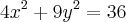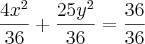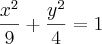por ah001334 » Dom Nov 13, 2011 19:00
por ah001334 » Dom Nov 13, 2011 19:00
Olá pessoal me ajudem na correção de alguns exercícios de cônicas.
-Identificar as cônicas representadas pelas equações, colocar na forma padrão se necessário, analisar se a cônica é centrada na origem ou se a mesma sofreu translação.
a) 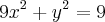
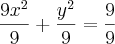
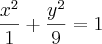
Raizes:

e

será uma elipse em R2 centrada na origem sendo que o eixo x é +-1 e eixo y +-3
-
ah001334
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Seg Out 17, 2011 12:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por ah001334 » Seg Nov 14, 2011 20:18
por ah001334 » Seg Nov 14, 2011 20:18
Ta certo ai pessoal, preciso corrigir os exercícios!!!
Me ajudem!!
-
ah001334
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Seg Out 17, 2011 12:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cônicas]Retas tangentes à cônicas
por Hopkins » Ter Fev 28, 2017 22:39
- 0 Respostas
- 1527 Exibições
- Última mensagem por Hopkins

Ter Fev 28, 2017 22:39
Geometria Analítica
-
- [Álgebra I, exercicios] Exercicios que estão sem resolução.
por vitorullmann » Ter Mar 05, 2013 21:26
- 0 Respostas
- 3299 Exibições
- Última mensagem por vitorullmann

Ter Mar 05, 2013 21:26
Álgebra Elementar
-
- Conicas
por baianinha » Qua Set 14, 2011 00:30
- 1 Respostas
- 1434 Exibições
- Última mensagem por LuizAquino

Qua Set 14, 2011 00:58
Álgebra Elementar
-
- Cônicas
 por Claudin » Dom Mai 13, 2012 12:43
por Claudin » Dom Mai 13, 2012 12:43
- 7 Respostas
- 3132 Exibições
- Última mensagem por Claudin

Dom Mai 20, 2012 23:08
Geometria Analítica
-
- Cônicas
por Claudin » Dom Mai 13, 2012 14:34
- 5 Respostas
- 2233 Exibições
- Última mensagem por Claudin

Dom Mai 20, 2012 20:03
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
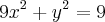
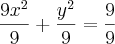
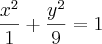
 e
e