 por vaninha » Qui Set 30, 2010 20:34
por vaninha » Qui Set 30, 2010 20:34
já tentei várias vezes resolver mas não acho uma solução...por onde começar...
como consigo calcular a altura de um cone equilátero se o exercício me deu só o volume que é 24pi?
-
vaninha
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Set 30, 2010 20:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por vaninha » Qui Set 30, 2010 20:37
por vaninha » Qui Set 30, 2010 20:37
vaninha escreveu:já tentei várias vezes resolver mas não acho uma solução...por onde começar...
como consigo calcular a altura de um cone equilátero se o exercício me deu só o volume que é 24pi?
-
vaninha
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Set 30, 2010 20:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Elcioschin » Sex Out 01, 2010 18:37
por Elcioschin » Sex Out 01, 2010 18:37
Fantini
Uma pequena correção
r³ = 24*V3 ----> (r³)² = 24²*3 ----> r^6 = (8*3)²*3 -----> r^6 = (2³*3)²*3 ----> r^6 = (2^6)*3³ ----> r = 2*V3
h = r*V3 ----> h = (2*V3)*V3 ----> h = 6
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por MarceloFantini » Sex Out 01, 2010 18:39
por MarceloFantini » Sex Out 01, 2010 18:39
Obrigado Elcio.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por vaninha » Seg Out 04, 2010 15:54
por vaninha » Seg Out 04, 2010 15:54
muitoO obrigadoO...
-
vaninha
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Set 30, 2010 20:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ME AJUDE POR FAVOR:Cilindro circular reto inscrito no cone
por netochaves » Sex Abr 05, 2013 14:32
- 0 Respostas
- 1832 Exibições
- Última mensagem por netochaves

Sex Abr 05, 2013 14:32
Cálculo: Limites, Derivadas e Integrais
-
- Cone (ITA - SP)
 por Ananda » Ter Fev 26, 2008 20:07
por Ananda » Ter Fev 26, 2008 20:07
- 3 Respostas
- 9671 Exibições
- Última mensagem por admin

Qua Fev 27, 2008 13:08
Geometria Espacial
-
- Cone
por Neperiano » Ter Mai 12, 2009 21:04
- 6 Respostas
- 3983 Exibições
- Última mensagem por Neperiano

Qui Mai 14, 2009 17:13
Geometria Espacial
-
- Cone
por GABRIELA » Sex Fev 12, 2010 16:09
- 2 Respostas
- 1862 Exibições
- Última mensagem por GABRIELA

Qui Fev 18, 2010 14:59
Geometria Espacial
-
- Cone
por DanielFerreira » Qua Jun 23, 2010 16:25
- 1 Respostas
- 1540 Exibições
- Última mensagem por MarceloFantini

Qui Jun 24, 2010 00:01
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




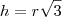 . Logo:
. Logo: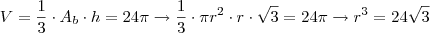
![r = 2 \cdot \sqrt[3]{3 \sqrt{3}} \rightarrow h = r \sqrt{3} = 2 \cdot \sqrt[3]{3 \sqrt{3}} \cdot \sqrt{3} = \sqrt[6]{27 \cdot 27} = \sqrt[6]{3^6} = 3 r = 2 \cdot \sqrt[3]{3 \sqrt{3}} \rightarrow h = r \sqrt{3} = 2 \cdot \sqrt[3]{3 \sqrt{3}} \cdot \sqrt{3} = \sqrt[6]{27 \cdot 27} = \sqrt[6]{3^6} = 3](/latexrender/pictures/776d20332512e399ebc2585b4c73f5f3.png)




