




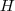 e
e  as alturas maior e menor respectivamente. Então
as alturas maior e menor respectivamente. Então  . A razão entre os volumes será o cubo da razão entre os segmentos, logo
. A razão entre os volumes será o cubo da razão entre os segmentos, logo 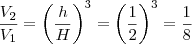 onde
onde 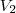 é o volume da pirâmide menor e
é o volume da pirâmide menor e 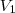 da pirâmide original. O raciocínio é análogo para as áreas.
da pirâmide original. O raciocínio é análogo para as áreas.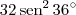 parece quase um chute.
parece quase um chute.

MarceloFantini escreveu:Sejame
as alturas maior e menor respectivamente. Então
. A razão entre os volumes será o cubo da razão entre os segmentos, logo
onde
é o volume da pirâmide menor e
da pirâmide original. O raciocínio é análogo para as áreas.
Como você chegou nesta resolução? Porque suas contas não fazem sentido, o valorparece quase um chute.

 , onde l é o lado do triângulo e h a altura dele.
, onde l é o lado do triângulo e h a altura dele.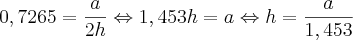
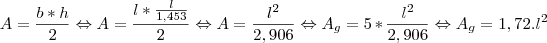
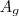 é a área do pentágono da pirâmide maior.
é a área do pentágono da pirâmide maior.
 é o lado do pentágono da pirâmide menor e
é o lado do pentágono da pirâmide menor e  é o lado do pentágono da pirâmide maior
é o lado do pentágono da pirâmide maior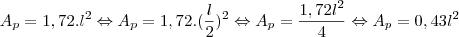




MickaelSantos escreveu:Primeiro eu dividi o pentágono da base em 5 triângulos e, chamando cada lado do pentágono de l, calculei a altura de cada triângulo assim:, onde l é o lado do triângulo e h a altura dele.
Desenvolvendo a expressão, cheguei em:
Depois calculei a área do triângulo e multipliquei por 5, que é a quantidade de triângulos do pentágono:
Onde:é a área do pentágono da pirâmide maior.
Então eu comparei a medida do lado do pentágono menor com a do pentágono maior, usando o Teorema de Tales:
Onde:é o lado do pentágono da pirâmide menor e
é o lado do pentágono da pirâmide maior
Obs. tenho dúvidas nessa parte!
Agora o cálculo da área do pentágono menor, usando a fórmula acima:
Agora a relação:
Isso quer dizer que a área do pentágono da pirâmide maior é 4 vezes a área do pentágono da pirâmide menor.
Acho que é isso...
Se alguém puder dar uma olhada e ver se está certo, principalmente na parte da relação entre o lado do maior e o lado do menor, agradeço.








Voltar para Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.