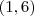 e tangente a reta
e tangente a reta 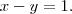

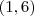 e tangente a reta
e tangente a reta 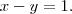

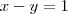

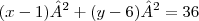

Claudin escreveu:Determine a equação da circunferencia com centroe tangente a reta
Claudin escreveu:Tentei fazer do seguinte modo
tendo a eq da tangente
descobri o ponto na reta tangente sendo
E fiz a distancia entre 2 pontos
e encontrei a equação como
Porém o resultado não é este.
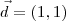 é o vetor diretor da reta, temos que:
é o vetor diretor da reta, temos que: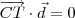
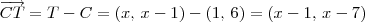
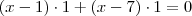





Claudin escreveu:Tive uma dúvida, gostaria de saber a técnica que você usa para encontrar vetor diretor d = (1,1), pois eu sempre erro, mudo um sinal que não devia mudar e por ai vai...
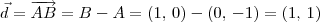


Claudin escreveu:No caso você atribuiu valores ne?
Quando x=0 e quando y=0
certo?


Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 .
.



