 por Bruhh » Sáb Nov 20, 2010 17:30
por Bruhh » Sáb Nov 20, 2010 17:30
Olá, Boa Tarde
Tenho o seguinte problema para resolver:
Se a mudança de base de B para A =

determine o vetor A onde o vetor B=

Resolvi assim:

=
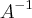
.

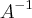
=

.

Mas aí está a minha dúvida, qual é o formato de uma matriz 3 linhas e 1 coluna?? Está correto
do jeito que estou resolvendo?
Obrigada
-
Bruhh
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Seg Mar 01, 2010 14:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Eng. Química
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Mudança de Base] Matriz de mudança de base ? para ?.
por fabriel » Ter Nov 26, 2013 15:38
- 0 Respostas
- 2108 Exibições
- Última mensagem por fabriel

Ter Nov 26, 2013 15:38
Álgebra Linear
-
- [Mudança de Base]
por ewald » Sex Abr 13, 2012 00:20
- 0 Respostas
- 1414 Exibições
- Última mensagem por ewald

Sex Abr 13, 2012 00:20
Introdução à Álgebra Linear
-
- MUDANÇA DE BASE
por renatoneumann » Qui Ago 29, 2013 16:58
- 1 Respostas
- 1590 Exibições
- Última mensagem por e8group

Qui Ago 29, 2013 18:46
Logaritmos
-
- Mudança de base
por Thalis » Qui Jul 24, 2014 01:34
- 1 Respostas
- 2497 Exibições
- Última mensagem por Pessoa Estranha

Qui Jul 24, 2014 23:31
Álgebra Linear
-
- logaritmos - mudança de base
por Raquel » Seg Mar 29, 2010 20:02
- 2 Respostas
- 7280 Exibições
- Última mensagem por rodrigorfg

Sáb Abr 10, 2010 01:26
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 determine o vetor A onde o vetor B=
determine o vetor A onde o vetor B=
 =
= 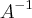 .
. 
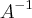 =
=  .
. 



 .
.
 :
: