 por ARCS » Sex Mai 20, 2011 08:59
por ARCS » Sex Mai 20, 2011 08:59
Estou com dificuldades neste caso. Já fiz diversos exercícios parecidos com este, mas este envolve somas vetoriais. Grato pela ajuda!
Sabendo que
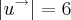
,
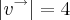
e 30º o ângulo formado entre u e v.
Calcular a área do paralelogramo determinado por u+v e u-v.
-
ARCS
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Qui Out 28, 2010 18:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Sex Mai 20, 2011 10:25
por LuizAquino » Sex Mai 20, 2011 10:25
DicasDados dois vetores
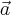
e
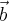
, temos que são válidas as afirmações abaixo.
(i) A área
A do paralelogramo determinado por esses vetores, sendo

o ângulo formado entre eles, é dada por

.
(ii)

(iii)

, sendo

o ângulo formado por esses vetores (não nulos).
(iv)

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Produto escalar, Produto Vetorial e Produto Misto
 por fernando7 » Qua Mai 23, 2018 17:29
por fernando7 » Qua Mai 23, 2018 17:29
- 0 Respostas
- 4949 Exibições
- Última mensagem por fernando7

Qua Mai 23, 2018 17:29
Geometria Analítica
-
- Produto vetorial
por ViniciusAlmeida » Seg Abr 27, 2015 20:36
- 0 Respostas
- 1325 Exibições
- Última mensagem por ViniciusAlmeida

Seg Abr 27, 2015 20:36
Geometria Analítica
-
- [G.A] Produto vetorial
por ViniciusAlmeida » Qui Abr 16, 2015 08:21
- 0 Respostas
- 1383 Exibições
- Última mensagem por ViniciusAlmeida

Qui Abr 16, 2015 08:21
Geometria Analítica
-
- Produto vetorial
por a1918842 » Qui Out 17, 2019 11:21
- 2 Respostas
- 8496 Exibições
- Última mensagem por adauto martins

Qui Out 17, 2019 20:34
Geometria Analítica
-
- Ajuda em Produto Vetorial
por Vini » Qui Out 22, 2009 11:59
- 0 Respostas
- 1580 Exibições
- Última mensagem por Vini

Qui Out 22, 2009 11:59
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
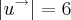 ,
, 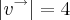 e 30º o ângulo formado entre u e v.
e 30º o ângulo formado entre u e v.
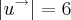 ,
, 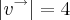 e 30º o ângulo formado entre u e v.
e 30º o ângulo formado entre u e v.
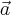 e
e 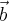 , temos que são válidas as afirmações abaixo.
, temos que são válidas as afirmações abaixo. o ângulo formado entre eles, é dada por
o ângulo formado entre eles, é dada por  .
.
 , sendo
, sendo  o ângulo formado por esses vetores (não nulos).
o ângulo formado por esses vetores (não nulos).

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.