Renato_RJ escreveu:Boa tarde campeão...
Vamos as definições, se uma reta é paralela a x=2 esta reta pode ser x=3, x =4, etc.. Mas não pode ser x=2, pois seriam a mesma reta !!!
No segundo problema, ele pede a reta da base menor, você descobriu a equação da reta da BASE MAIOR, a base menor é o segmento DC, refaça as contas.... Só uma coisa, eu não entendi o porque da matriz e a coordenada z ter valor igual a 1 (a não ser que você esteja usando um plano paralelo a xy com altura z=1), pois pelo que me consta, um trapézio tem pelo menos dois lados paralelos, logo AB é paralelo a DC, se C tem coordenada (6,5) D terá (x,5) então sua reta seria y = 5...
Abraços e boa sorte nas contas...
Renato.
1ª questãoNa verdade a reta pode ser x =2, até por o enunciado diz isso, e a resposta oferecida pelo autor do livro também da x = 2 como resposta, eu apenas queria entender porque.
2ª questãoO valor de z sendo igual a 1 se deve a
forma segmentaria da equação da reta 
, considerando um ponto generico

, e fazendo:

Eu analisei novamente o desenho do gráfico e conclui, sendo D (x,5) como dito por você, e as retas paralelas da base maior com a base menor

, ou seja, por
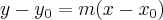


A 2ª questão eu compreendi, mas a 1ª ainda não.

 , não tenho ideia de como chegar nesse resultado.
, não tenho ideia de como chegar nesse resultado.





 , considerando um ponto generico
, considerando um ponto generico  , e fazendo:
, e fazendo: 
 , ou seja, por
, ou seja, por 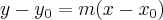


 , com
, com  ou
ou  )
)  .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
