 por jcmatematica » Qua Jul 30, 2014 00:51
por jcmatematica » Qua Jul 30, 2014 00:51
Qual é o valor de K para que o resto da divisão de 2x³ - 5x² + Kx - 2 por x + 2i seja 18 + 14i?
Minha resolução chegou em k = 1.
Será que está correto?
-
jcmatematica
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Ter Jul 29, 2014 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matematica
- Andamento: formado
 por e8group » Qui Jul 31, 2014 13:33
por e8group » Qui Jul 31, 2014 13:33
Vamos checar !
Dizer que o polinômio (dado) dividido por
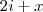
deixa resto
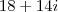
implica que em dizer que existe algum polinômio

tal que
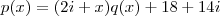
(onde p é o polinômio dado) .
Avaliando p em x = - 2i , tem-se que
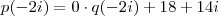
.o valor de k requerido é a solução da equação :
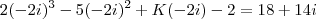
que é k = 1 .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por jcmatematica » Sáb Ago 02, 2014 15:59
por jcmatematica » Sáb Ago 02, 2014 15:59
Valeu
-
jcmatematica
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Ter Jul 29, 2014 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matematica
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Valor de Mercadoria] A partir do valor total de venda
por Gerson Belini » Qua Out 02, 2013 02:17
- 0 Respostas
- 3906 Exibições
- Última mensagem por Gerson Belini

Qua Out 02, 2013 02:17
Matemática Financeira
-
- [Calcule o valor de Seno de 18º] Expressar o valor numérico
por VictorFPS » Sáb Fev 14, 2015 20:01
- 1 Respostas
- 3868 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:41
Trigonometria
-
- valor bruto a partir do valor liquido
por juan cunha » Ter Mai 03, 2016 10:29
- 3 Respostas
- 17801 Exibições
- Última mensagem por nakagumahissao

Sáb Mai 07, 2016 22:51
Matemática Financeira
-
- Valor de i que maximiza o valor do lucro
por filipeferminiano » Qui Jun 23, 2011 14:41
- 3 Respostas
- 4591 Exibições
- Última mensagem por LuizAquino

Sáb Ago 27, 2011 22:45
Cálculo
-
- valor da distribuição e valor da esperança
por Ana Maria da Silva » Sex Abr 11, 2014 00:12
- 1 Respostas
- 2479 Exibições
- Última mensagem por fff

Sex Abr 11, 2014 15:31
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



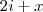 deixa resto
deixa resto 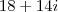 implica que em dizer que existe algum polinômio
implica que em dizer que existe algum polinômio  tal que
tal que 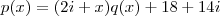 (onde p é o polinômio dado) .
(onde p é o polinômio dado) . 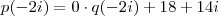 .o valor de k requerido é a solução da equação :
.o valor de k requerido é a solução da equação : 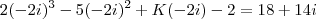 que é k = 1 .
que é k = 1 .

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.