 por marioitalo » Qua Out 15, 2008 20:26
por marioitalo » Qua Out 15, 2008 20:26
Olá a todos,
Estive lendo a resolução de um problema que consistia em provar que
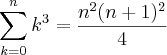
, o que é equivalente a
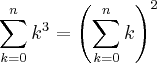
Pois bem, acontece que o primeiro passo para quem elaborou o gabarito foi transformar

em
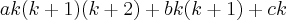
Não consigo entender de onde saiu essa expressão. Consegui enxergar apenas que
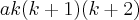
foi fatorado de
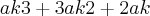
, que
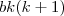
foi fatorado de
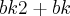
e
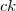
de
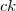
Alguém pode me socorrer, porque estou há um tempão tentando enxergar de onde surgiu esse desdobramento, se foi baseado em algum teorema, se foi por derivada, integral, intuição... O pior é que deve ser algo bem banal e tá me deixando maluco.
-
marioitalo
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Out 15, 2008 20:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia em Sistemas da Computação
- Andamento: cursando
 por admin » Sex Out 17, 2008 05:33
por admin » Sex Out 17, 2008 05:33
Olá
marioitalo, boas-vindas!
Somente partindo desta expansão em particular eu ainda também não percebi qual foi a expressão considerada inicialmente e o objetivo na demonstração. Talvez a idéia fique mais clara enviando a resolução completa para apreciarmos.
Vale dizer que não há apenas uma prova ou demonstração para esta soma de cubos, há várias.
Não sei se sua dúvida é apenas esta ou se a idéia de outra demonstração ajudaria.
Por exemplo, uma possibilidade é considerar a seguinte expansão:
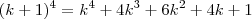
E antes de variarmos

de

a

, escrevemos assim:
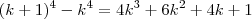
Fazendo

variar, temos:
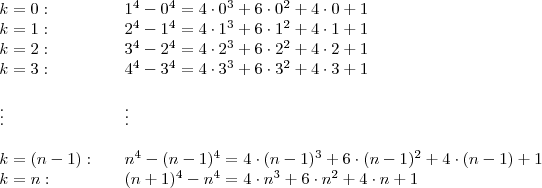
Repare que somando todos os membros, do lado esquerdo teremos vários cancelamentos, e do lado direito colocamos em evidência a soma dos cubos, dos quadrados e dos naturais:

Chamando de


Agora consideramos a soma dos quadrados obtida de forma análoga:
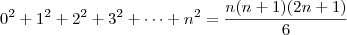
E também esta mais comum:

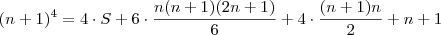
Expandindo a quarta potência, fazendo as outras distributivas e isolando

, obtemos:
![S = \left[ \frac{n(n+1)}{2} \right]^2 S = \left[ \frac{n(n+1)}{2} \right]^2](/latexrender/pictures/4821ca5ca58652f298baeddc25359095.png)
Até mais!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por marioitalo » Sex Out 17, 2008 15:41
por marioitalo » Sex Out 17, 2008 15:41
Muito obrigado pela resposta e pelas boas vindas, Fabio.
Segue abaixo o desenvolvimento completo da questão.
Obs.: Eu consegui chegar à expressão

fazendo a expansão de
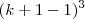
, como se fosse
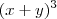
considerando
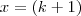
e
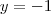
e rearrumando os termos, mas ainda assim não sei como se chegou àquela outra expressão.
Abraço.
Editado pela última vez por
marioitalo em Sex Out 17, 2008 23:41, em um total de 1 vez.
-
marioitalo
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Out 15, 2008 20:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia em Sistemas da Computação
- Andamento: cursando
 por admin » Sex Out 17, 2008 18:03
por admin » Sex Out 17, 2008 18:03
Olá
marioitalo!
Agora a idéia criativa da demonstração ficou mais clara.
Antes, um detalhe de edição que percebi: na segunda parte, 2ª e 3ª linhas, faltou o símbolo fatorial em

.
Sobre a sua dúvida para a escolha de

daquela forma, podemos dizer que sim, foi uma "intuição" tática.
A origem desta idéia surge ao observar onde queremos chegar, ou seja:
![S = \left[ \frac{n(n+1)}{2} \right]^2 S = \left[ \frac{n(n+1)}{2} \right]^2](/latexrender/pictures/4821ca5ca58652f298baeddc25359095.png)
Em destaque, este produto:
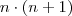
.
Quem criou a demonstração queria "fazer surgir" fatoriais para após as simplificações ficar com o produto
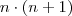
.
Note que

pode ser representado de outras formas conforme conveniência na prova.
Como aquela foi a escolha, estas são as condições para que a expressão se mantenha verdadeira:
De modo que os termos de grau 2 e 1 sejam anulados, ficando o de grau 3 com coeficiente 1:
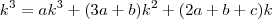
Há outras demonstrações também bem interessantes e criativas. Li sobre uma geométrica que consta no livro do Simmons, cálculo com geometria analítica. Meu livro deve chegar na próxima semana, caso não tenha e queira ver posso postar depois por aqui.
Bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por marioitalo » Dom Out 19, 2008 03:05
por marioitalo » Dom Out 19, 2008 03:05
Olá Fabio,
Desculpe a demora em responder, mas é que comecei a seguir uma série de sites sobre o assunto que me levaram até aqui:
http://en.wikipedia.org/wiki/Pochhammer_symbol, uma página da Wikipedia falando sobre o símbolo de Pochhammer, que representa o "rising sequential product" ou fatorial ascendente (não sei se a tradução é exatamente essa), que guarda grande similaridade com a tal expressão inicial que postei. Pesquisando mais um puco, cheguei a esse PDF:
http://www.escolademestres.com/qedtexte/tomo1serieamostra.pdf, um manual de seqüências e séries. Lá pela página 14 ele resolve o mesmo problema usando o tal produto fatorial, com a diferença que lá ele usa o descendente e naquela demonstração que postei acredito que tenha sido usado o ascendente.
É mais ou menos assim: Seja
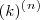
um polinômio fatorial da forma
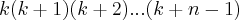
Considerando que:
Podemos exprimir um polinômio
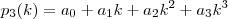
em função dos polinômios fatoriais
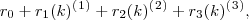
sendo
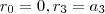
e

os restos das divisões abaixo:
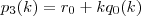

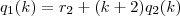
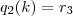
Achando esses restos
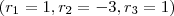
, já caimos direto na expressão que foi utilizada dentro do somatório na resolução postada anteriormente, qual seja:
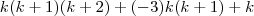
Se não quisermos obter esses restos, basta atribuir

como foi feito naquele primeiro caso e, ao final, zerarmos os coeficientes de
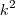
e
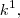
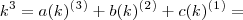
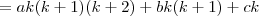
E aqui finalmente a bendita expressão aparece!
Bem, é isso. Se eu escrevi alguma besteira, por favor me corrijam...
Obrigado pela ajuda, Fabio.
Abraço.
-
marioitalo
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Out 15, 2008 20:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia em Sistemas da Computação
- Andamento: cursando
 por admin » Ter Out 28, 2008 15:40
por admin » Ter Out 28, 2008 15:40
Olá
marioitalo!
Também peço desculpas pela demora em responder, mas atualmente não estou tão presente por aqui.
Eu também não conhecia aquela forma simplificada de representar os produtos.
É mais uma evidência da necessidade em cálculos deste tipo, visando facilitar a notação.
Aproveito para dar parabéns ao seu interesse em pesquisar!
Eu havia comentado sobre uma demonstração geométrica que consta no livro do Simmons, veja que interessante.
Antes, o autor destaca que a prova partindo desta expressão
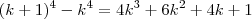
é apenas uma extensão da idéia "do grande teólogo-matemático-cientista-escritor francês Blaise Pascal" que provou a fórmula para a soma dos

primeiros quadrados a partir desta expansão:

Eis a demonstração geométrica:
Começando no ponto

, assentamos segmentos sucessivos de comprimentos
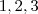
etc. e finalmente um de comprimento

atingindo o ponto

.
Fazemos o mesmo sobre a reta

perpendicular a
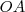
, de modo que
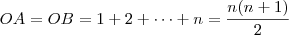
A área do quadrado é, portanto,
![S = \left[ \frac{n(n+1)}{2} \right]^2 \;\;\;\;\;\;\;\;\;\; (I) S = \left[ \frac{n(n+1)}{2} \right]^2 \;\;\;\;\;\;\;\;\;\; (I)](/latexrender/pictures/ef1e8ba07673690d2ed033da1ee52ff1.png)
Entretanto, o quadrado é a soma de

regiões em forma de
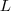
, indicadas na figura:
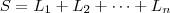
Qual é a área de

? Essa região pode ser dividida em dois retângulos, como na figura. Assim
![L_n = n \left[ \frac{n(n+1)}{2} \right] + n \left[ \frac{(n-1)n}{2} \right] L_n = n \left[ \frac{n(n+1)}{2} \right] + n \left[ \frac{(n-1)n}{2} \right]](/latexrender/pictures/dc5e67880aa252f02d42941ed68fe34a.png)
![= \frac12 n^2 \left[ (n+1)+(n-1) \right] = n^3 = \frac12 n^2 \left[ (n+1)+(n-1) \right] = n^3](/latexrender/pictures/498ab8afa9df2fb164437055465b4ad7.png)
Conseqüentemente,
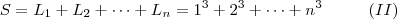
e comparando
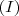
e
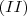
temos
![1^3 + 2^3 + \cdots + n^3 = \left[ \frac{n(n+1)}{2} \right]^2 1^3 + 2^3 + \cdots + n^3 = \left[ \frac{n(n+1)}{2} \right]^2](/latexrender/pictures/0bd14a9561c0c92449b75c5655e22aa0.png)
Bons estudos e até mais!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Transformação Linear] Nucleo e Imagem, ache a transformaçao
por vualas » Qua Nov 07, 2012 00:37
- 2 Respostas
- 4248 Exibições
- Última mensagem por adauto martins

Qui Dez 15, 2016 11:12
Álgebra Linear
-
- [polinômio]Relações de Girard + raízes de polinômio
por matano2104 » Qui Set 05, 2013 17:02
- 1 Respostas
- 7157 Exibições
- Última mensagem por young_jedi

Qui Set 05, 2013 17:57
Polinômios
-
- Transformação
por barbara-rabello » Ter Nov 20, 2012 14:30
- 1 Respostas
- 1847 Exibições
- Última mensagem por MarceloFantini

Ter Nov 20, 2012 15:02
Álgebra Linear
-
- transformação
por zenildo » Qui Jun 05, 2014 23:53
- 1 Respostas
- 2725 Exibições
- Última mensagem por Russman

Sex Jun 06, 2014 01:53
Conversão de Unidades
-
- Transformação em produto
 por Ananda » Seg Mar 24, 2008 17:31
por Ananda » Seg Mar 24, 2008 17:31
- 3 Respostas
- 5514 Exibições
- Última mensagem por Ananda

Ter Mar 25, 2008 14:55
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Dom Jan 17, 2010 14:42
Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?

O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois

2°) Admitamos que

, seja verdadeira:

(hipótese da indução)
e provemos que

Temos: (Nessa parte)

Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Seg Jan 18, 2010 01:55
Boa noite Fontelles.
Não sei se você está familiarizado com o
Princípio da Indução Finita, portanto vou tentar explicar aqui.
Ele dá uma equação, no caso:

E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:

Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que

seja verdadeiro, e pretendemos provar que também é verdadeiro para

.




Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.
Espero ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Seg Jan 18, 2010 02:28
Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Qui Jan 21, 2010 11:32
Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Jan 21, 2010 12:25
Boa tarde Fontelles!
Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.
O que temos que provar é isso:

, certo? O autor começou do primeiro membro:

Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:

Que é outra verdade. Agora, com certeza:

Agora, como

é

a

, e este por sua vez é sempre

que

, logo:

Inclusive, nunca é igual, sempre maior.
Espero (dessa vez) ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Caeros - Dom Out 31, 2010 10:39
Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?
Assunto:
Princípio da Indução Finita
Autor:
andrefahl - Dom Out 31, 2010 11:37
c.q.d. = como queriamos demonstrar =)
Assunto:
Princípio da Indução Finita
Autor:
Abelardo - Qui Mai 05, 2011 17:33
Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Mai 05, 2011 20:05
Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Assunto:
Princípio da Indução Finita
Autor:
Vennom - Qui Abr 26, 2012 23:04
MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa.

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
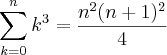 , o que é equivalente a
, o que é equivalente a 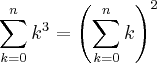
 em
em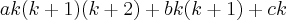
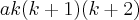 foi fatorado de
foi fatorado de 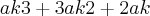 , que
, que 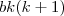 foi fatorado de
foi fatorado de 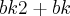 e
e 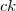 de
de 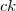


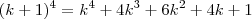
 de
de  a
a  , escrevemos assim:
, escrevemos assim: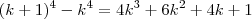
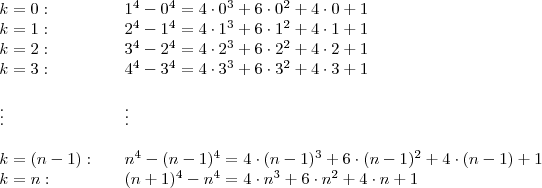



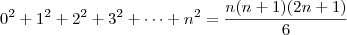

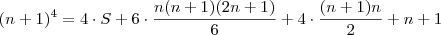
 , obtemos:
, obtemos:![S = \left[ \frac{n(n+1)}{2} \right]^2 S = \left[ \frac{n(n+1)}{2} \right]^2](/latexrender/pictures/4821ca5ca58652f298baeddc25359095.png)

 fazendo a expansão de
fazendo a expansão de 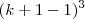 , como se fosse
, como se fosse 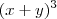 considerando
considerando 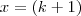 e
e 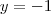 e rearrumando os termos, mas ainda assim não sei como se chegou àquela outra expressão.
e rearrumando os termos, mas ainda assim não sei como se chegou àquela outra expressão.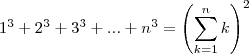

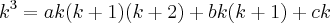
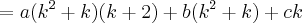
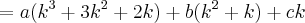
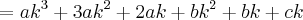
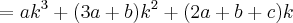

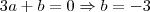



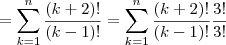
![=3!\sum_{k=1}^{n}\frac{(k+2)!}{(k-1)!3!}=3![C(3,3)+...+C(n+2,3)] =3!\sum_{k=1}^{n}\frac{(k+2)!}{(k-1)!3!}=3![C(3,3)+...+C(n+2,3)]](/latexrender/pictures/0f32f69c690f7d5eeba58eaefe11a409.png)
![=3![C(n+3,4)] =3![C(n+3,4)]](/latexrender/pictures/3bc0ff02fadcd0c7585a8e2ce37f28a7.png) (pelo teorema das colunas do triângulo de Pascal)
(pelo teorema das colunas do triângulo de Pascal)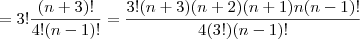
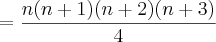
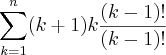
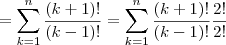
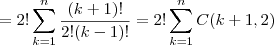
![=2![C(2,2)+C(3,2)+...+C(n+1,2)]=2![C(n+2,3)] =2![C(2,2)+C(3,2)+...+C(n+1,2)]=2![C(n+2,3)]](/latexrender/pictures/5049f994e27110d41dfe241cfc50e923.png) (pelo teorema das colunas)
(pelo teorema das colunas)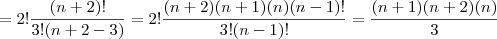
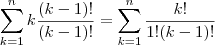
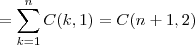 (pelo teorema das colunas)
(pelo teorema das colunas)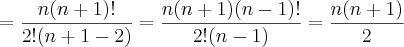
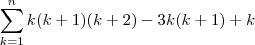
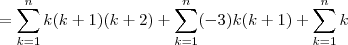
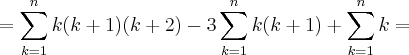
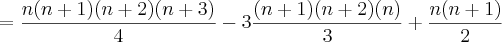

![=\frac{n(n+1)[3(n+2)(n+3)-12(n+2)+6n]}{12} =\frac{n(n+1)[3(n+2)(n+3)-12(n+2)+6n]}{12}](/latexrender/pictures/9bccca4cf5f59885edb45684aa6dc608.png)
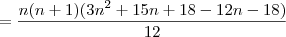
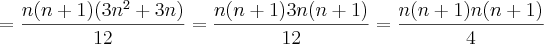
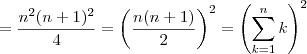
 .
. .
.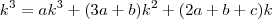
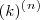 um polinômio fatorial da forma
um polinômio fatorial da forma 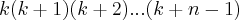
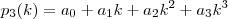 em função dos polinômios fatoriais
em função dos polinômios fatoriais 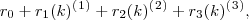 sendo
sendo 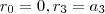 e
e  os restos das divisões abaixo:
os restos das divisões abaixo: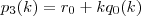

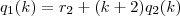
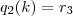
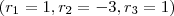 , já caimos direto na expressão que foi utilizada dentro do somatório na resolução postada anteriormente, qual seja:
, já caimos direto na expressão que foi utilizada dentro do somatório na resolução postada anteriormente, qual seja: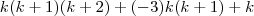
 como foi feito naquele primeiro caso e, ao final, zerarmos os coeficientes de
como foi feito naquele primeiro caso e, ao final, zerarmos os coeficientes de 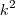 e
e 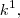
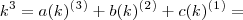
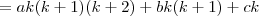

 , assentamos segmentos sucessivos de comprimentos
, assentamos segmentos sucessivos de comprimentos 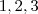 etc. e finalmente um de comprimento
etc. e finalmente um de comprimento  .
. perpendicular a
perpendicular a  , de modo que
, de modo que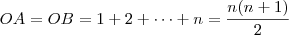
![S = \left[ \frac{n(n+1)}{2} \right]^2 \;\;\;\;\;\;\;\;\;\; (I) S = \left[ \frac{n(n+1)}{2} \right]^2 \;\;\;\;\;\;\;\;\;\; (I)](/latexrender/pictures/ef1e8ba07673690d2ed033da1ee52ff1.png)
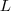 , indicadas na figura:
, indicadas na figura: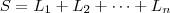
 ? Essa região pode ser dividida em dois retângulos, como na figura. Assim
? Essa região pode ser dividida em dois retângulos, como na figura. Assim![L_n = n \left[ \frac{n(n+1)}{2} \right] + n \left[ \frac{(n-1)n}{2} \right] L_n = n \left[ \frac{n(n+1)}{2} \right] + n \left[ \frac{(n-1)n}{2} \right]](/latexrender/pictures/dc5e67880aa252f02d42941ed68fe34a.png)
![= \frac12 n^2 \left[ (n+1)+(n-1) \right] = n^3 = \frac12 n^2 \left[ (n+1)+(n-1) \right] = n^3](/latexrender/pictures/498ab8afa9df2fb164437055465b4ad7.png)
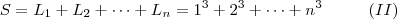
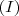 e
e 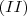 temos
temos![1^3 + 2^3 + \cdots + n^3 = \left[ \frac{n(n+1)}{2} \right]^2 1^3 + 2^3 + \cdots + n^3 = \left[ \frac{n(n+1)}{2} \right]^2](/latexrender/pictures/0bd14a9561c0c92449b75c5655e22aa0.png)


 , seja verdadeira:
, seja verdadeira: (hipótese da indução)
(hipótese da indução)



 .
.





 é
é  a
a  , e este por sua vez é sempre
, e este por sua vez é sempre  que
que  , logo:
, logo:
