 por SARG » Seg Abr 25, 2011 22:50
por SARG » Seg Abr 25, 2011 22:50
Olá! É a primeira vez que estou participando do fórum, (espero estar fazendo da maneira correta...rs).
Tenho bastante dificuldade de trabalhar com divisões com variaveis com potência. Gostaria de saber como posso solucionar a quastão abaixo e se existe algum tipo de regra geral, quando o divisor é = 1.
Dado o polinômio A(x) =
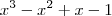
, obtemos o quociente

e o resto

quando dividido pelo polinômio B(x). Para
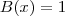
,

será igual a?
Desde já, agradeço atenção, estou precisando bastante desta resposta.]
Bjos.
-
SARG
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Abr 25, 2011 22:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: CIENCIAS CONTABEIS
- Andamento: cursando
 por FilipeCaceres » Seg Abr 25, 2011 23:22
por FilipeCaceres » Seg Abr 25, 2011 23:22
Você precisa saber que:
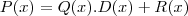
No teu caso temos,
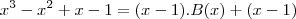
Observe que tanto o lado esquerdo quanto o lado direito devem ser iguais, sendo assim devemos ter
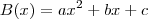
,ou seja, deve ser do 2º grau.
Portanto,
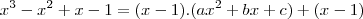
Agora basta você realizar as operações apenas no lado direito e depois igualar os coeficientes.
Ex.:
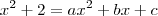



Qualquer dúvida poste novamente.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por LuizAquino » Seg Abr 25, 2011 23:31
por LuizAquino » Seg Abr 25, 2011 23:31
O exercício consiste em determinar os valores de x para os quais B(x)=1.
Isso significa que devemos resolver a equação
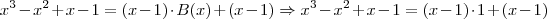
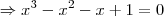
Note que x=1 é uma raiz dessa equação. Para achar as outras raízes, basta dividir
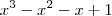
por

, o que resulta em
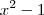
. Portanto, temos que
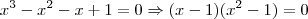
Desse última equação obtemos que as raízes são x=1 e x=-1.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por SARG » Seg Abr 25, 2011 23:40
por SARG » Seg Abr 25, 2011 23:40
Muito obrigada, vou ter que treinar um pouco para chegar a resposta sozinha, mas, a ajuda de vocês foi de muita valia. Obrigada mais uma vez.
-
SARG
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Abr 25, 2011 22:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: CIENCIAS CONTABEIS
- Andamento: cursando
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Divisão de polinômios
por manuoliveira » Dom Nov 14, 2010 14:00
- 1 Respostas
- 2595 Exibições
- Última mensagem por VtinxD

Seg Nov 15, 2010 01:13
Polinômios
-
- Divisão de Polinômios
por -civil- » Seg Mai 30, 2011 20:31
- 3 Respostas
- 2438 Exibições
- Última mensagem por -civil-

Seg Mai 30, 2011 21:20
Cálculo: Limites, Derivadas e Integrais
-
- divisão de polinomios
por theSinister » Seg Mai 23, 2011 17:11
- 6 Respostas
- 3911 Exibições
- Última mensagem por theSinister

Seg Mai 23, 2011 22:34
Álgebra Elementar
-
- Divisão de Polinômios
por Claudin » Qua Ago 03, 2011 20:25
- 3 Respostas
- 2187 Exibições
- Última mensagem por Claudin

Qui Ago 04, 2011 15:46
Polinômios
-
- Divisão de polinômios
por Gaules » Qua Out 19, 2011 16:47
- 0 Respostas
- 1416 Exibições
- Última mensagem por Gaules

Qua Out 19, 2011 16:47
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
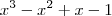 , obtemos o quociente
, obtemos o quociente  e o resto
e o resto  quando dividido pelo polinômio B(x). Para
quando dividido pelo polinômio B(x). Para 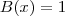 ,
,  será igual a?
será igual a?

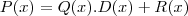
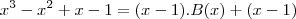
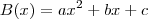 ,ou seja, deve ser do 2º grau.
,ou seja, deve ser do 2º grau. 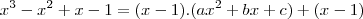
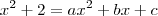




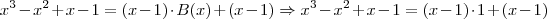
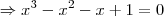
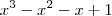 por
por  , o que resulta em
, o que resulta em 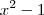 . Portanto, temos que
. Portanto, temos que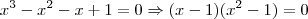


 .
.



