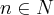, uma pessoa passa uma nota de R$10,00 a uma segunda pessoa como troco de uma compra, esta segunda pessoa por sua vez passa esta mesma nota a uma terceira pessoa e assim sucessivamente. Determine a probabilidade de esta nota ser passada m vezes, m 
, 
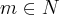, sem retornar a primeira pessoa.Gabarito:
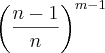
Pessoal, não faço nem ideia de como faz essa questão. Alguém pode resolver e explicar para mim? Obrigado desde já.
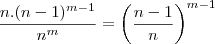
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)