 por cynderella » Dom Jan 10, 2010 09:26
por cynderella » Dom Jan 10, 2010 09:26
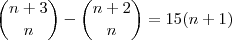
Olà eu tentei fazer este exercicio,mas gostaria de saber se é assim ?Se não for puderiam-me explicar?
A minha resolução:

-
cynderella
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Jan 10, 2010 07:05
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: informatica
- Andamento: cursando
 por Cleyson007 » Dom Jan 10, 2010 12:28
por Cleyson007 » Dom Jan 10, 2010 12:28
Cynderella seja bem vinda ao Ajuda Matemática!
Pelo que entendi, o problema quer que encontre os valores de n.
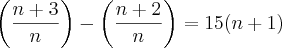
Cynderella, note que invertendo o sinal de - (fora do parêntese), inverto os demais sinais dentro do parêntese, veja:
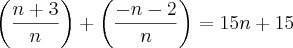
Tirando o mínimo, temos:
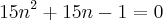
Para encontrar os valores de n, basta reolver a equação do 2º grau.
Vamos ver se alguém tem algo a dizer.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Molina » Dom Jan 10, 2010 12:48
por Molina » Dom Jan 10, 2010 12:48
Boa tarde, Cleyson.
Acho que o que está dentro do parênteses não é uma fração e sim uma combinação.
Achei que é isso por dois motivos:
i) não há o traço da divisão.
ii) o local onde a questão foi postada.
Abraços,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por cynderella » Dom Jan 10, 2010 16:09
por cynderella » Dom Jan 10, 2010 16:09
Boa tarde Neylson eu gostaria dizer que este exercicio é uma combinação, mas ja agora agradeço pela tua resposta que deste se mesmo assim puderes ajudar-me eu fico agradecida.
-
cynderella
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Jan 10, 2010 07:05
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: informatica
- Andamento: cursando
 por Cleyson007 » Dom Jan 10, 2010 16:15
por Cleyson007 » Dom Jan 10, 2010 16:15
molina escreveu:Acho que o que está dentro do parênteses não é uma fração e sim uma combinação.
Achei que é isso por dois motivos:
i) não há o traço da divisão.
ii) o local onde a questão foi postada.
Abraços,

Boa tarde Molina e Cynderella!
Desculpe, não percebi que era uma combinação

Montei a combinação:
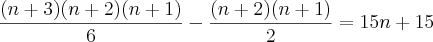
Tentei resolver, mas os valores que encontrei para n não satisfazem a combinação.
Como estão tentando resolver?
Vamos ver onde estamos errando..

Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Molina » Seg Jan 11, 2010 23:36
por Molina » Seg Jan 11, 2010 23:36
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Cleyson007 » Qua Jan 13, 2010 23:31
por Cleyson007 » Qua Jan 13, 2010 23:31
Boa tarde Molina!
Molina, desculpe por não ter dado meu parecer quanto sua resolução, mas foi o corre-corre da vida..

Achei o seu método de resolução menos trabalhoso que o meu.
Apresento minha resolução (apesar de não ter encontrado asi raízes que satisfaçam o problema), veja só:
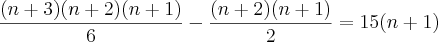
Tirando o mínimo:
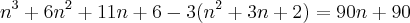
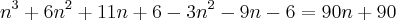
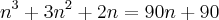

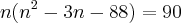
Minha dúvida é se posso fazer o seguinte: Igualar as duas partes com o 90


Bom, as raízes dessa equação não satisfazem as condições do problema. A minha intenção é saber onde está o meu erro, ok?
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por MarceloFantini » Qui Jan 14, 2010 02:15
por MarceloFantini » Qui Jan 14, 2010 02:15
Boa noite Cleyson!
O seu erro está aqui:
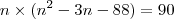
Você não pode afirmar que

. Veja este exemplo:
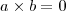
. Neste caso, você pode afirmar que um dos fatores é igual a zero pois esta é a única maneira. Agora veja este:
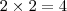
. Só porque o produto é quatro não significa que um dos seus fatores seja 4.
Sobre a questão de combinação, eu fui no wolfram alpha pra resolver a equação de terceiro grau, e ele plotou esse gráfico:

Estou começando a acreditar que esta questão não tem resposta.
Espero ter ajudado.
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Dúvida ANOVA] Uma dúvida sobre a estatística correta
por gustamfar » Ter Mai 22, 2018 18:19
- 0 Respostas
- 11058 Exibições
- Última mensagem por gustamfar

Ter Mai 22, 2018 18:19
Estatística
-
- Dúvida PA
por Cleyson007 » Dom Jun 01, 2008 01:01
- 2 Respostas
- 10770 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:38
Progressões
-
- Dúvida
por miguelbaptista » Sex Jan 09, 2009 03:29
- 8 Respostas
- 12545 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:13
Logaritmos
-
- dúvida
por gdarius » Dom Ago 16, 2009 00:09
- 1 Respostas
- 3159 Exibições
- Última mensagem por Felipe Schucman

Dom Ago 16, 2009 02:35
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida!!
por GABRIELA » Qui Set 17, 2009 18:19
- 5 Respostas
- 5735 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:38
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
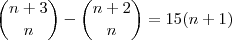


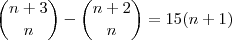


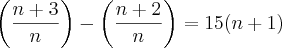
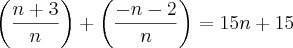
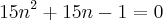





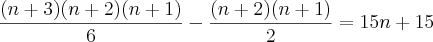


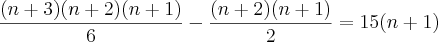
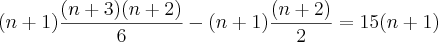
![(n+1)\left[ \frac{(n+3)(n+2)}{6}-\frac{(n+2)}{2} \right]=15(n+1) (n+1)\left[ \frac{(n+3)(n+2)}{6}-\frac{(n+2)}{2} \right]=15(n+1)](/latexrender/pictures/308154ee557eb5772c56a5c90963465e.png)
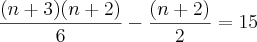
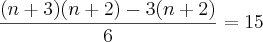
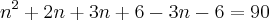
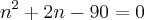



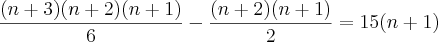
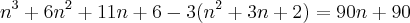
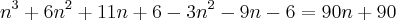
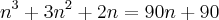

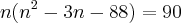



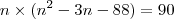
 . Veja este exemplo:
. Veja este exemplo: 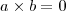 . Neste caso, você pode afirmar que um dos fatores é igual a zero pois esta é a única maneira. Agora veja este:
. Neste caso, você pode afirmar que um dos fatores é igual a zero pois esta é a única maneira. Agora veja este: 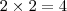 . Só porque o produto é quatro não significa que um dos seus fatores seja 4.
. Só porque o produto é quatro não significa que um dos seus fatores seja 4.


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
