 por Walquiria » Dom Nov 13, 2011 23:04
por Walquiria » Dom Nov 13, 2011 23:04
x-y=1
x^2+y^2= 8,5
Sendo x>0 e y>0, a soma x+y vale: Resposta:4
-
Walquiria
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Dom Abr 03, 2011 11:54
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: formado
 por Walquiria » Seg Nov 14, 2011 10:35
por Walquiria » Seg Nov 14, 2011 10:35
NÃO ENTENDI SUA RESOLUÇÃO????????????????
-
Walquiria
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Dom Abr 03, 2011 11:54
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: formado
 por MarceloFantini » Seg Nov 14, 2011 18:08
por MarceloFantini » Seg Nov 14, 2011 18:08
Primeiramente, sabemos que
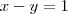
. Elevei ambos ao quadrado e usando que
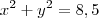
, conclui que
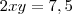
. Queremos saber o valor de

, logo, experimentei calcular o seu valor ao quadrado:
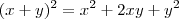
. Usando novamente a informação do enunciado e o dado que acabei de encontrar, temos
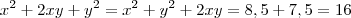
. Então
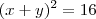
, e portanto
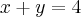
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- sistemas de equãções
por Rejane Sampaio » Sex Set 12, 2008 23:54
- 1 Respostas
- 2671 Exibições
- Última mensagem por admin

Ter Set 16, 2008 20:31
Estatística
-
- Sistemas de equações
por Danilo Dias Vilela » Qua Set 09, 2009 17:34
- 1 Respostas
- 1278 Exibições
- Última mensagem por Molina

Qua Set 09, 2009 17:54
Sistemas de Equações
-
- Sistemas de equações
por Danilo Dias Vilela » Qua Set 09, 2009 21:19
- 1 Respostas
- 1442 Exibições
- Última mensagem por Elcioschin

Qua Set 09, 2009 22:27
Sistemas de Equações
-
- Sistemas de equações
por Danilo Dias Vilela » Qua Set 09, 2009 23:55
- 1 Respostas
- 2304 Exibições
- Última mensagem por Molina

Qui Set 10, 2009 14:15
Sistemas de Equações
-
- Sistemas de equações
por Danilo Dias Vilela » Qui Set 10, 2009 00:25
- 2 Respostas
- 2274 Exibições
- Última mensagem por RICI

Sex Ago 24, 2012 11:58
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





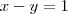 . Elevei ambos ao quadrado e usando que
. Elevei ambos ao quadrado e usando que 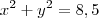 , conclui que
, conclui que 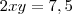 . Queremos saber o valor de
. Queremos saber o valor de  , logo, experimentei calcular o seu valor ao quadrado:
, logo, experimentei calcular o seu valor ao quadrado: 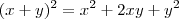 . Usando novamente a informação do enunciado e o dado que acabei de encontrar, temos
. Usando novamente a informação do enunciado e o dado que acabei de encontrar, temos 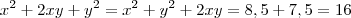 . Então
. Então 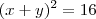 , e portanto
, e portanto 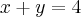 .
.


 .
.



