 por Alessandrasouza » Ter Mai 18, 2010 18:59
por Alessandrasouza » Ter Mai 18, 2010 18:59
Oie gente..entaum.. eu to com uma dúvida de novoo...na verdade é outra pro meesmo assuunto.. É um problema de PA q eu resolvi mas acho q tá muito grande a resolução e nem sei se está de fato correto..É assim:
Alexandre comprou um album com espaço para 660 figurinhas. Td dia ele compra 20 pacotinhos, sendo 5 figurinhas em kd uma. No 1º dia ele colocou todas. No 2º dia, vieram algumas repetidas e colocou 95. No 3º 90 e assim por diante. Calcule o tempo necessáriop/ preencher o album...
E eu fiz assim:
Sn =

660=

660=
![\frac{[100+(100+(n-1)-5)].n}{2} \frac{[100+(100+(n-1)-5)].n}{2}](/latexrender/pictures/8df70cb7e2040c23ba7fb64f483a30a2.png)
660=
![\frac{[100+100-5n+5].n}{2} \frac{[100+100-5n+5].n}{2}](/latexrender/pictures/e5af354d52ced4fa9254e8be095bded4.png)
660=
![\frac{[205-5n].n}{2} \frac{[205-5n].n}{2}](/latexrender/pictures/b306ca4da5f432c1107fad3ba1e3a752.png)
2.(660)= 205n-5
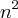
1320= 205n-5
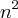
0=-1320+205n-5
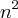
dividi td por -5 p/ simplificar
0=264-41n+1
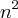
virou uma equação de 2ºgrau a=1 b=-41 c=264
resolvendo a equação de 2ºgrau têm-se que
n1=33 n2=8Por isso, eu quero saber se naum tem um jeito de fazer que seja menor....
-
Alessandrasouza
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Mai 14, 2010 15:10
- Formação Escolar: EJA
- Área/Curso: ensino médio
- Andamento: cursando
 por MarceloFantini » Ter Mai 18, 2010 23:07
por MarceloFantini » Ter Mai 18, 2010 23:07
O jeito analítico acredito que seja somente esse, mas você pode fazer a soma no braço (não é tão grande).
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Cleyson007 » Qua Mai 19, 2010 19:17
por Cleyson007 » Qua Mai 19, 2010 19:17
Boa noite Alessandra e Fantini!
Também não consegui desenvolver outra forma de resolução (acredito que se houver outra forma, não irá fugir muito de P.A...)
O resultado está correto! é interessante observar que a P.A. é decrescente, portanto,

.
Achei interessante que a resolução cai numa equação do 2º grau... portanto, duas raízes reais (valores de n).
Fiquei com uma dúvida: "Como se explica o fato de possuírem dos valores que satisfazem (algebricamente) a condição?"Acredito que a resposta coerente para esse tipo de exercício seja
8 dias.. quando o Alexandre chegar no 33º dia, as figurinhas já não estariam todas coladas?
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por MarceloFantini » Qui Mai 20, 2010 02:24
por MarceloFantini » Qui Mai 20, 2010 02:24
Porque eles satisfazem a equação. Lembre-se que a equação não sabe do problema, nós é que sabemos da situação real representada pela equação.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (UNIFOR) Progressão Aritmética e Progressão Harmônica
por andersontricordiano » Ter Mar 22, 2011 12:56
- 1 Respostas
- 6141 Exibições
- Última mensagem por LuizAquino

Ter Mar 22, 2011 13:52
Progressões
-
- Progressão aritmética e progressão geométrica
por Danilo Dias Vilela » Sex Mar 12, 2010 13:41
- 1 Respostas
- 4730 Exibições
- Última mensagem por thadeu

Sex Mar 12, 2010 17:36
Progressões
-
- [Aritmética] Progressão Aritmética.
por Pessoa Estranha » Qua Ago 28, 2013 22:11
- 2 Respostas
- 5634 Exibições
- Última mensagem por Pessoa Estranha

Qui Ago 29, 2013 16:06
Aritmética
-
- Progressão Aritmética
por Rejane Sampaio » Qua Set 17, 2008 16:20
- 1 Respostas
- 4430 Exibições
- Última mensagem por juliomarcos

Qui Set 18, 2008 13:07
Álgebra Elementar
-
- Progressão Aritmética (PA)
por Cleyson007 » Ter Jan 27, 2009 21:40
- 2 Respostas
- 8408 Exibições
- Última mensagem por Cleyson007

Sáb Mai 30, 2009 12:31
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![\frac{[100+(100+(n-1)-5)].n}{2} \frac{[100+(100+(n-1)-5)].n}{2}](/latexrender/pictures/8df70cb7e2040c23ba7fb64f483a30a2.png)
![\frac{[100+100-5n+5].n}{2} \frac{[100+100-5n+5].n}{2}](/latexrender/pictures/e5af354d52ced4fa9254e8be095bded4.png)
![\frac{[205-5n].n}{2} \frac{[205-5n].n}{2}](/latexrender/pictures/b306ca4da5f432c1107fad3ba1e3a752.png)
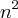
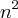
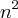 dividi td por -5 p/ simplificar
dividi td por -5 p/ simplificar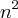 virou uma equação de 2ºgrau a=1 b=-41 c=264
virou uma equação de 2ºgrau a=1 b=-41 c=264



 .
.

