 por Joana Gabriela » Seg Ago 02, 2010 15:04
por Joana Gabriela » Seg Ago 02, 2010 15:04
Outra dúvidaa...
Resolva a equação 2+5+8+...+x=77, sabendo que os termos do 1ºmembro estão em PA.
Minha resolução:
x=n
Sn= (a1 + an).n
2
77= (2+ 2 + (n-1).3).n
2
154= (4 + 3n - 3).n
154= 3n² + n
.....
-
Joana Gabriela
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Jul 28, 2010 10:13
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Agroecologia
- Andamento: cursando
 por MarceloFantini » Qui Ago 05, 2010 16:50
por MarceloFantini » Qui Ago 05, 2010 16:50
Só falta resolver o polinômio do segundo grau.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Joana Gabriela » Sex Ago 06, 2010 15:55
por Joana Gabriela » Sex Ago 06, 2010 15:55
Mas eu não consigo resolver !
-
Joana Gabriela
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Jul 28, 2010 10:13
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Agroecologia
- Andamento: cursando
 por Molina » Sex Ago 06, 2010 16:13
por Molina » Sex Ago 06, 2010 16:13
Joana Gabriela escreveu:Mas eu não consigo resolver !
Bastava resolver a equação de segundo grau:
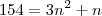

Usando a fórmula de Bhaskara:
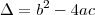
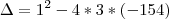
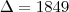
Agora precisamos encontrar as raízes:
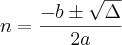
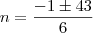
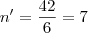
e
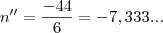
Como n precisa ser positivo, ficamos com a resposta de

.
Sugiro você revisar equações do 2° grau. Bom estudo!
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por MarceloFantini » Seg Ago 09, 2010 12:25
por MarceloFantini » Seg Ago 09, 2010 12:25
Não coloque duas dúvidas num mesmo tópico, crie um novo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Molina » Seg Ago 09, 2010 14:42
por Molina » Seg Ago 09, 2010 14:42
Boa tarde, Joana Gabriela.
Como nosso amigo Fantini disse, crie apenas uma questão por tópico, a não ser que sua dúvida seja relacionada ao exercício proposto, por exemplo algo que não ficou bem explicado ou algum agradecimento a ser feito. Isso é uma forma de manter o fórum mais organizado, pois outras pessoas podem conter a mesma dúvida que você. Caso queira colocar uma nova dúvida (como aconteceu agora) crie um novo tópico. OK?
Sua nova questão foi movida para cá: viewtopic.php?f=110&t=2566
Qualquer dúvida me procure.
Faça bom uso deste ambiente! 
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Joana Gabriela » Ter Ago 10, 2010 17:25
por Joana Gabriela » Ter Ago 10, 2010 17:25
ok
-
Joana Gabriela
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Jul 28, 2010 10:13
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Agroecologia
- Andamento: cursando
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação - Dúvida básica sobre a proporcionalidade de equação
por FelipeGM » Qui Jan 12, 2012 19:05
- 4 Respostas
- 7734 Exibições
- Última mensagem por FelipeGM

Sáb Jan 14, 2012 13:16
Álgebra Elementar
-
- Equação - como montar a equação desse problema?
por _Manu » Qua Jul 04, 2012 03:37
- 7 Respostas
- 13237 Exibições
- Última mensagem por _Manu

Qui Jul 05, 2012 01:49
Sistemas de Equações
-
- [Equação polinomial] Ajuda com essa equação?
por Mkdj21 » Sáb Jan 26, 2013 16:19
- 1 Respostas
- 13026 Exibições
- Última mensagem por young_jedi

Dom Jan 27, 2013 17:15
Equações
-
- [Equação da reta] Encontrando equação paramétrica.
por Vitor Sanches » Qua Jun 26, 2013 17:54
- 0 Respostas
- 6098 Exibições
- Última mensagem por Vitor Sanches

Qua Jun 26, 2013 17:54
Geometria Analítica
-
- Equação - Como resolver problema com equação
por macedo1967 » Seg Set 25, 2017 10:13
- 3 Respostas
- 8713 Exibições
- Última mensagem por DanielFerreira

Dom Out 08, 2017 20:10
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





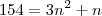

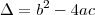
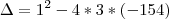
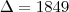
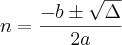
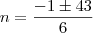
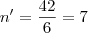
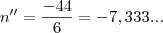
 .
.









