 por andersontricordiano » Dom Jul 24, 2011 17:05
por andersontricordiano » Dom Jul 24, 2011 17:05
Sabe-se que

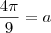
.
a)Qual é o sinal de

? Justifique.
b)Calcule, em função de

,

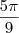
.
c)Calcule

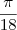
e
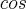
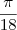
Respostas:
a) positivo, pois
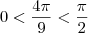
b)

c)

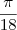


![\sqrt[]{1-a^2} \sqrt[]{1-a^2}](/latexrender/pictures/4efea669ba5135241509e21e66d378bb.png)
e
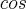
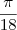
Agradeço muito quem resolver!
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por FilipeCaceres » Dom Jul 24, 2011 18:01
por FilipeCaceres » Dom Jul 24, 2011 18:01
Não irei resolver, mas vou lhe dar uma dica:
a) Em qual quadrante se encontra
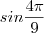
?
b)Reduça
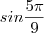
para o primeiro quadrante e analise.
c)Sabemos que
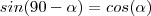
, logo
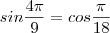
Também sabemos que:
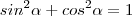
com isso você encontrará o valor de
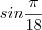
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculo de trigonometria
 por andersontricordiano » Seg Jun 06, 2011 17:13
por andersontricordiano » Seg Jun 06, 2011 17:13
- 1 Respostas
- 5625 Exibições
- Última mensagem por claudinho

Sáb Jun 11, 2011 05:27
Geometria
-
- Calculo de trigonometria
por andersontricordiano » Qua Jun 29, 2011 19:37
- 1 Respostas
- 1255 Exibições
- Última mensagem por Molina

Qua Jun 29, 2011 20:30
Trigonometria
-
- Pre-Universitario (Calculo de Trigonometria)
por Pre-Universitario » Seg Ago 08, 2011 17:32
- 2 Respostas
- 1763 Exibições
- Última mensagem por Pre-Universitario

Ter Ago 09, 2011 16:27
Trigonometria
-
- (Calculo de trigonometria) Calcule sen x - cos x
por andersontricordiano » Seg Ago 08, 2011 18:45
- 1 Respostas
- 1469 Exibições
- Última mensagem por DanielFerreira

Dom Abr 01, 2012 16:14
Trigonometria
-
- (Calculo de trigonometria da UF-MS adaptado)
por andersontricordiano » Ter Dez 06, 2011 14:53
- 2 Respostas
- 1905 Exibições
- Última mensagem por sabaku

Ter Dez 06, 2011 23:26
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

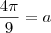 .
. ? Justifique.
? Justifique. ,
, 
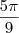 .
.
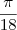 e
e 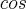
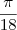
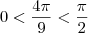


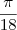


![\sqrt[]{1-a^2} \sqrt[]{1-a^2}](/latexrender/pictures/4efea669ba5135241509e21e66d378bb.png) e
e 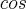
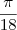


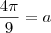 .
. ? Justifique.
? Justifique. ,
, 
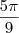 .
.
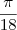 e
e 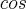
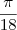
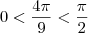


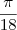


![\sqrt[]{1-a^2} \sqrt[]{1-a^2}](/latexrender/pictures/4efea669ba5135241509e21e66d378bb.png) e
e 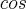
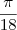

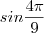 ?
?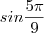 para o primeiro quadrante e analise.
para o primeiro quadrante e analise.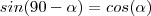 , logo
, logo 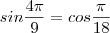
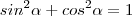 com isso você encontrará o valor de
com isso você encontrará o valor de 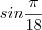


 .
.
 :
: