Como preparação para um teste, há dois exercícios do mesmo género de trigonometria que consistem em relacionar as razões trigonométricas, de forma a provar que um dos membros é igual ao outro.
Enunciado: Sendo x a amplitude de um ângulo agudo, mostra que:
1) sen x +
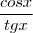 =
= 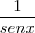
2)
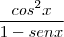 - 1 = sen x
- 1 = sen xGostaria que me indicassem a correcção, e posteriormente, truques para a resolução deste género de exercícios
Agradecido,
Luís Soares (couldzao).


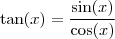 . Assim,
. Assim,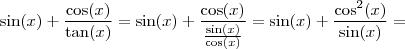
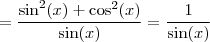 .
.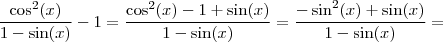
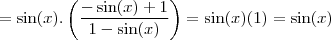


 .
.
 :
: