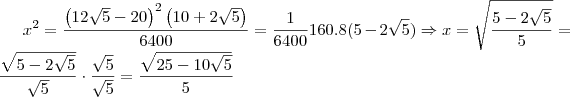por andersonlopes_bg » Qua Ago 01, 2012 18:34
por andersonlopes_bg » Qua Ago 01, 2012 18:34
O exercício é para calcular o sen
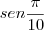
consegui calcular
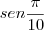
=
![\frac{\sqrt[2]{5}-1}{4} \frac{\sqrt[2]{5}-1}{4}](/latexrender/pictures/8ddc20bff8e75598b1afaab2701d506a.png)
e
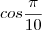
=
![\frac{\sqrt[2]{10+2\sqrt[2]{5}}}{4} \frac{\sqrt[2]{10+2\sqrt[2]{5}}}{4}](/latexrender/pictures/5ea34d5a248ad1165db3a3c8609c46e6.png)
, a tangente fica igual a =
![\frac{\sqrt[2]{5}-1}{\sqrt[2]{10+2\sqrt[2]{5}}} \frac{\sqrt[2]{5}-1}{\sqrt[2]{10+2\sqrt[2]{5}}}](/latexrender/pictures/79778b53d90183bcc072f708eff41313.png)
mas não consigo simplificar a resposta que é
![\frac{\sqrt[2]{25-10\sqrt[2]{5}}}{5} \frac{\sqrt[2]{25-10\sqrt[2]{5}}}{5}](/latexrender/pictures/cadf91c7cc4d915621c1116d9551c571.png)
. Obrigado!
-
andersonlopes_bg
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Set 30, 2011 20:29
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Informática
- Andamento: formado
 por Russman » Qua Ago 01, 2012 20:59
por Russman » Qua Ago 01, 2012 20:59
Basta você multiplicar a tangente por
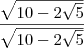
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Qui Ago 02, 2012 09:51
por Russman » Qui Ago 02, 2012 09:51
Não, o seno foi calculado certo.
É conhecido que que o Triângulo Isósceles Dourado, isto é, um triângulo Isósceles que o quociente entre seu maior lado e menor é a Razão Dourada, tem o ângulo de vértice iguala 36 graus e os de base 72 graus.
Assim,
![sin(\frac{36}{2}=18) = sin(\frac{\pi }{10}) =\frac{\left [ base \right ]}{2\left [ lado \right ]} \equiv \frac{1}{2\varphi } sin(\frac{36}{2}=18) = sin(\frac{\pi }{10}) =\frac{\left [ base \right ]}{2\left [ lado \right ]} \equiv \frac{1}{2\varphi }](/latexrender/pictures/e55307f3011dbd29dcedb9653653d847.png)
Como
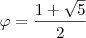
, segue o resultado
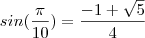
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Qui Ago 02, 2012 09:55
por Russman » Qui Ago 02, 2012 09:55
Pensando melhor, para simplificar a tangente eu suponho multiplicar primeiro por
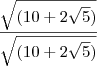
pra nos livrarmos da raíz quadrada.
Em seguida, multiplique por
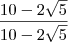
.
Então vai obter a resposta.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Qui Ago 02, 2012 10:24
por Russman » Qui Ago 02, 2012 10:24
Vou tentar simplificar/racionalizar aqui e já posto o que eu obtive.
Editado pela última vez por
Russman em Qui Ago 02, 2012 10:27, em um total de 1 vez.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Qui Ago 02, 2012 10:26
por Russman » Qui Ago 02, 2012 10:26
O processo é bem longo, mas felizmente obtemos a resposta esperada.
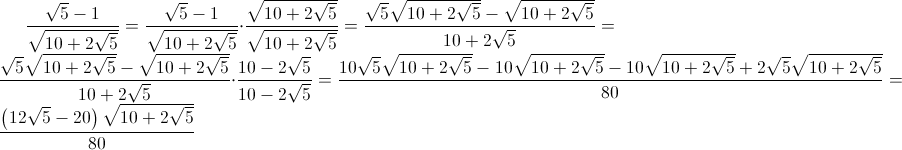
- CodeCogsEqn.gif (6.65 KiB) Exibido 1970 vezes
Agora, seja
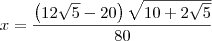
, então
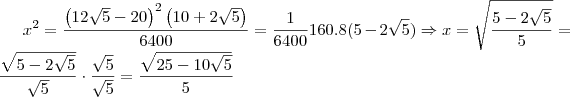
que é o resultado que bate com o gabarito.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por andersonlopes_bg » Qui Ago 02, 2012 12:21
por andersonlopes_bg » Qui Ago 02, 2012 12:21
Vixe! Não conseguiria chegar a esse resultado rsrs... Obrigado!!
-
andersonlopes_bg
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Set 30, 2011 20:29
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Informática
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ARCOS
por MERLAYNE » Qua Abr 04, 2012 23:28
- 1 Respostas
- 1556 Exibições
- Última mensagem por MarceloFantini

Qua Abr 04, 2012 23:54
Trigonometria
-
- Arcos - ITA
por DanielFerreira » Dom Abr 29, 2012 21:13
- 1 Respostas
- 1581 Exibições
- Última mensagem por nakagumahissao

Dom Abr 29, 2012 23:28
Trigonometria
-
- Arcos e radianos
por Micheline » Qua Jan 28, 2009 10:13
- 7 Respostas
- 6866 Exibições
- Última mensagem por Sandra Piedade

Dom Fev 01, 2009 10:08
Trigonometria
-
- Trigonometria-Arcos
por rodsales » Sex Abr 17, 2009 21:27
- 2 Respostas
- 2217 Exibições
- Última mensagem por rodsales

Sáb Abr 18, 2009 16:57
Trigonometria
-
- Exercício Arcos
por Cleyson007 » Sáb Mar 27, 2010 01:12
- 2 Respostas
- 1942 Exibições
- Última mensagem por Cleyson007

Dom Mar 28, 2010 11:02
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
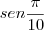 consegui calcular
consegui calcular 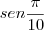 =
= ![\frac{\sqrt[2]{5}-1}{4} \frac{\sqrt[2]{5}-1}{4}](/latexrender/pictures/8ddc20bff8e75598b1afaab2701d506a.png) e
e 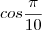 =
= ![\frac{\sqrt[2]{10+2\sqrt[2]{5}}}{4} \frac{\sqrt[2]{10+2\sqrt[2]{5}}}{4}](/latexrender/pictures/5ea34d5a248ad1165db3a3c8609c46e6.png) , a tangente fica igual a =
, a tangente fica igual a = ![\frac{\sqrt[2]{5}-1}{\sqrt[2]{10+2\sqrt[2]{5}}} \frac{\sqrt[2]{5}-1}{\sqrt[2]{10+2\sqrt[2]{5}}}](/latexrender/pictures/79778b53d90183bcc072f708eff41313.png) mas não consigo simplificar a resposta que é
mas não consigo simplificar a resposta que é ![\frac{\sqrt[2]{25-10\sqrt[2]{5}}}{5} \frac{\sqrt[2]{25-10\sqrt[2]{5}}}{5}](/latexrender/pictures/cadf91c7cc4d915621c1116d9551c571.png) . Obrigado!
. Obrigado!
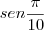 consegui calcular
consegui calcular 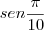 =
= ![\frac{\sqrt[2]{5}-1}{4} \frac{\sqrt[2]{5}-1}{4}](/latexrender/pictures/8ddc20bff8e75598b1afaab2701d506a.png) e
e 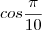 =
= ![\frac{\sqrt[2]{10+2\sqrt[2]{5}}}{4} \frac{\sqrt[2]{10+2\sqrt[2]{5}}}{4}](/latexrender/pictures/5ea34d5a248ad1165db3a3c8609c46e6.png) , a tangente fica igual a =
, a tangente fica igual a = ![\frac{\sqrt[2]{5}-1}{\sqrt[2]{10+2\sqrt[2]{5}}} \frac{\sqrt[2]{5}-1}{\sqrt[2]{10+2\sqrt[2]{5}}}](/latexrender/pictures/79778b53d90183bcc072f708eff41313.png) mas não consigo simplificar a resposta que é
mas não consigo simplificar a resposta que é ![\frac{\sqrt[2]{25-10\sqrt[2]{5}}}{5} \frac{\sqrt[2]{25-10\sqrt[2]{5}}}{5}](/latexrender/pictures/cadf91c7cc4d915621c1116d9551c571.png) . Obrigado!
. Obrigado!

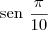 ? Talvez tenha errado nestas contas.
? Talvez tenha errado nestas contas.

![sin(\frac{36}{2}=18) = sin(\frac{\pi }{10}) =\frac{\left [ base \right ]}{2\left [ lado \right ]} \equiv \frac{1}{2\varphi } sin(\frac{36}{2}=18) = sin(\frac{\pi }{10}) =\frac{\left [ base \right ]}{2\left [ lado \right ]} \equiv \frac{1}{2\varphi }](/latexrender/pictures/e55307f3011dbd29dcedb9653653d847.png)
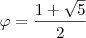 , segue o resultado
, segue o resultado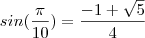

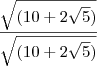
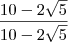 .
.

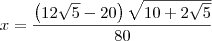 , então
, então