Se
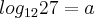 , então
, então 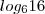 será igual a quanto?
será igual a quanto?


 e
e 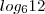 na última igualdade acima, perfeitamente possível, por quê?
na última igualdade acima, perfeitamente possível, por quê?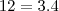 , aplique a propriedade logarítmica que transforma logaritmo de produto em soma de logaritmos.
, aplique a propriedade logarítmica que transforma logaritmo de produto em soma de logaritmos.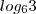 para o primeiro membro da igualdade que desenvolveu em (3).
para o primeiro membro da igualdade que desenvolveu em (3).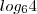 no segundo membro.
no segundo membro. 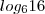 .
. .
. 

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

