(PASES/2000) Sejam as funções reais f, g e h definidas por
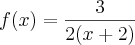
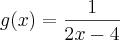 e
e 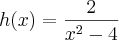
Se S = {x ? R|f(x) = g(x) - h(x)}, então é CORRETO afirmar que o conjunto S:
Resposta: é o conjunto vazio
Resolução:
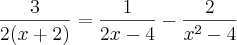 --> Tirando o MMC do segundo membro, fica
--> Tirando o MMC do segundo membro, fica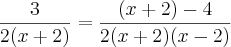 --> Multiplicando cruzado
--> Multiplicando cruzado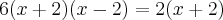
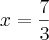
Não seria o conjunto unitário?


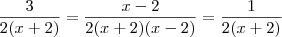 para
para  . Isto não é verdade para nenhum
. Isto não é verdade para nenhum  , portanto é o conjunto vazio.
, portanto é o conjunto vazio.

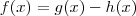 , e não existe nenhum. Olhe a expressão que eu cheguei e teste: tomemos
, e não existe nenhum. Olhe a expressão que eu cheguei e teste: tomemos  . Então teremos
. Então teremos 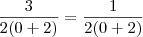 , que é falso. Qualquer valor real que você substituir será falso. Lembre-se que
, que é falso. Qualquer valor real que você substituir será falso. Lembre-se que  pela existência das funções, logo não existem valores reais satisfazendo a igualdade.
pela existência das funções, logo não existem valores reais satisfazendo a igualdade.
 .
.
 :
: