 por Rafael16 » Qua Ago 15, 2012 12:54
por Rafael16 » Qua Ago 15, 2012 12:54
Boa tarde pessoal,
(PASES/2000) Sejam as funções reais f, g e h definidas por
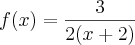
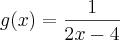
e
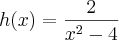
Se S = {x ? R|f(x) = g(x) - h(x)}, então é CORRETO afirmar que o conjunto S:
Resposta: é o conjunto vazio
Resolução:
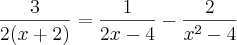
--> Tirando o MMC do segundo membro, fica
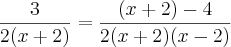
--> Multiplicando cruzado
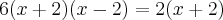
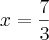
Não seria o conjunto unitário?
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por MarceloFantini » Qua Ago 15, 2012 13:06
por MarceloFantini » Qua Ago 15, 2012 13:06
Note que
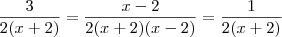
para

. Isto não é verdade para nenhum

, portanto é o conjunto vazio.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Rafael16 » Qua Ago 15, 2012 13:24
por Rafael16 » Qua Ago 15, 2012 13:24
MarceloFantini escreveu: Isto não é verdade para nenhum

, portanto é o conjunto vazio.
Isso quer dizer que só vai ser absurdo o x = -2 para 2 das 3 funções? Por isso ser a solução o conjunto vazio?
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por MarceloFantini » Qua Ago 15, 2012 14:03
por MarceloFantini » Qua Ago 15, 2012 14:03
Você não deve pensar nas funções isoladamente, mas sim com a condição do enunciado. Devemos encontrar os valores reais tais que
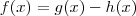
, e não existe nenhum. Olhe a expressão que eu cheguei e teste: tomemos

. Então teremos
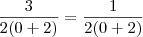
, que é falso. Qualquer valor real que você substituir será falso. Lembre-se que

pela existência das funções, logo não existem valores reais satisfazendo a igualdade.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Funções] Questão Vestibular UFV PASES 2010
por ronaldoudi » Qua Out 12, 2011 23:06
- 0 Respostas
- 1222 Exibições
- Última mensagem por ronaldoudi

Qua Out 12, 2011 23:06
Sistemas de Equações
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5214 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
-
- [plano tangente a função de duas variaveis dada por função]
por isaac naruto » Qui Dez 31, 2015 16:35
- 0 Respostas
- 4339 Exibições
- Última mensagem por isaac naruto

Qui Dez 31, 2015 16:35
Cálculo: Limites, Derivadas e Integrais
-
- [Desigualdade] entre função exponencial e função potência
por VitorFN » Sex Mai 26, 2017 15:18
- 1 Respostas
- 5437 Exibições
- Última mensagem por adauto martins

Sex Jul 07, 2017 12:17
Álgebra Elementar
-
- +uma função das trevas.ajuda aew!(função par mas heim!?)
por Fabricio dalla » Dom Fev 27, 2011 16:12
- 2 Respostas
- 3337 Exibições
- Última mensagem por LuizAquino

Dom Mar 06, 2011 09:17
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
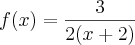
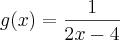 e
e 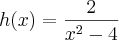
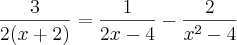 --> Tirando o MMC do segundo membro, fica
--> Tirando o MMC do segundo membro, fica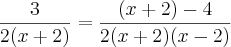 --> Multiplicando cruzado
--> Multiplicando cruzado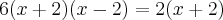
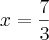


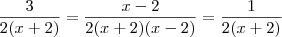 para
para  . Isto não é verdade para nenhum
. Isto não é verdade para nenhum  , portanto é o conjunto vazio.
, portanto é o conjunto vazio.

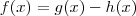 , e não existe nenhum. Olhe a expressão que eu cheguei e teste: tomemos
, e não existe nenhum. Olhe a expressão que eu cheguei e teste: tomemos  . Então teremos
. Então teremos 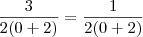 , que é falso. Qualquer valor real que você substituir será falso. Lembre-se que
, que é falso. Qualquer valor real que você substituir será falso. Lembre-se que  pela existência das funções, logo não existem valores reais satisfazendo a igualdade.
pela existência das funções, logo não existem valores reais satisfazendo a igualdade. .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
