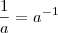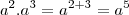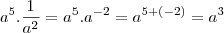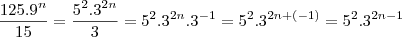por Raphael Feitas10 » Ter Abr 12, 2011 01:10
por Raphael Feitas10 » Ter Abr 12, 2011 01:10
Determine o valor de n de modo que,o quociente entre os inteiros positivos da forma [

,admita 18 divisores.R:3
Tentei mas ñ conseguie achar esse resultado brother,me ajuda aew parceiro...fiz ate aqui...

-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por FilipeCaceres » Ter Abr 12, 2011 01:30
por FilipeCaceres » Ter Abr 12, 2011 01:30
O quociente entre os inteiros positivos da forma
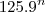
e 15,admita 18 divisores
Assim temos

Portanto,



Espero ter ajudado.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Raphael Feitas10 » Ter Abr 12, 2011 01:43
por Raphael Feitas10 » Ter Abr 12, 2011 01:43
filipecaceres escreveu:O quociente entre os inteiros positivos da forma
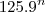
e 15,admita 18 divisores
Assim temos

Portanto,



Espero ter ajudado.
Pelo que eu entendie vc simplificou as duas espressões né,mas ñ entendie esse -1 aew me explica melhor aew brother desde ja muito obrg por ter respondido me ajudou e muito...
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por FilipeCaceres » Ter Abr 12, 2011 01:52
por FilipeCaceres » Ter Abr 12, 2011 01:52
Observe que,

Conseguiu entender?
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Raphael Feitas10 » Ter Abr 12, 2011 13:56
por Raphael Feitas10 » Ter Abr 12, 2011 13:56
filipecaceres escreveu:Observe que,

Conseguiu entender?
Abraço.
brother ñ entendie ainda de onde saio esse -1 da expresão 2n-1...
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por FilipeCaceres » Ter Abr 12, 2011 14:55
por FilipeCaceres » Ter Abr 12, 2011 14:55
Vou tentar lhe mostrar de uma outra forma, veja
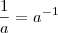
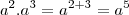
Agora veja,
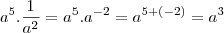
Na questão temos,
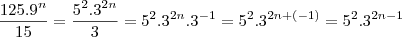
Espero que tenha entendido agora.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Numeros primos mutlipos e divisiros 24
por Raphael Feitas10 » Sex Fev 25, 2011 01:17
- 4 Respostas
- 2046 Exibições
- Última mensagem por Renato_RJ

Sex Fev 25, 2011 14:50
Funções
-
- Numeros primos mutlipos e divisiros 26
por Raphael Feitas10 » Ter Mar 29, 2011 15:16
- 1 Respostas
- 889 Exibições
- Última mensagem por FilipeCaceres

Ter Mar 29, 2011 16:47
Sistemas de Equações
-
- Numeros primos mutlipos e divisiros 43
por Raphael Feitas10 » Sex Ago 12, 2011 01:46
- 1 Respostas
- 888 Exibições
- Última mensagem por LuizAquino

Sex Ago 12, 2011 08:25
Sistemas de Equações
-
- [Teoria Números] Algoritmo Não Interceptação Números Primos
por WillamesSilva » Qua Out 26, 2016 12:21
- 8 Respostas
- 17203 Exibições
- Última mensagem por WillamesSilva

Ter Nov 22, 2016 15:33
Aritmética
-
- Números primos
 por mony0771 » Qui Abr 23, 2009 10:54
por mony0771 » Qui Abr 23, 2009 10:54
- 2 Respostas
- 4110 Exibições
- Última mensagem por mony0771

Qui Abr 23, 2009 15:28
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ,admita 18 divisores.R:3
,admita 18 divisores.R:3

 ,admita 18 divisores.R:3
,admita 18 divisores.R:3

e 15,admita 18 divisores





e 15,admita 18 divisores