Uma construtora tem que colocar postes telegráficos ao longo de uma estrada.Se os colocar a 25 metros de distância uns dos outros,fatam-lhe 150 postes; se os colacar a 30 metros,sobram-lhe 70 postes.Calcule o numero de poste e qual o comprimento da estrada:R 1170 e 3300m
Brother ñ conseguei interpretar essa questão pra chegar na resposta me ajuda aew por favor...


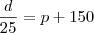 , coloquei +150 pois é o que deveríamos ter para dar certo.
, coloquei +150 pois é o que deveríamos ter para dar certo.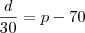 ,coloquei -70 pois do total de postes deveríamos retirar 70 para dar certo.
,coloquei -70 pois do total de postes deveríamos retirar 70 para dar certo.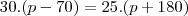
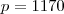
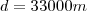


 , avisa que eu resolvo.
, avisa que eu resolvo.

