 por Fabricio dalla » Sáb Fev 26, 2011 18:49
por Fabricio dalla » Sáb Fev 26, 2011 18:49
nao consegui resolver essa funçao pra determinar o intervalo positivo e real dela (eu fiz o zero da funçao achei m=3/2 mas acho q ta errado)algume me ajuda ai por favor. agradeço a atençao de todos!
o conjunto de todos os valores de m para os quais a funçao
![f(x)=\frac{{x}^{2}+(2m+3)x+({m}^{2}+3)}{\sqrt[2]{{x}^{2}+(2m+1)x+({m}^{2}+2)}} f(x)=\frac{{x}^{2}+(2m+3)x+({m}^{2}+3)}{\sqrt[2]{{x}^{2}+(2m+1)x+({m}^{2}+2)}}](/latexrender/pictures/1bd31fa69bc1c0007fb84f855ca01f35.png)
esta definida e é nao-negativa para todo x real é :
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Sáb Fev 26, 2011 20:16
por Molina » Sáb Fev 26, 2011 20:16
Boa noite, Fabrício.
Editei sua função a cima, pois assim a fração fica melhor.
Para que esta função esteja definida o denominador (parte de baixo da fração) tem que ser maior que zero. Assim:
![\sqrt[2]{{x}^{2}+(2m+1)x+({m}^{2}+2)}>0 \sqrt[2]{{x}^{2}+(2m+1)x+({m}^{2}+2)}>0](/latexrender/pictures/bc1981117145f4e3c4a4f251658bdb84.png)
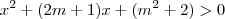
...
Ache as raízes desta equação. Como o coeficiente de

é positivo, os valores maiores que zero desta equação será os valores entre as raízes.
Para encontrar os valores em que a função seja não negativa, ou seja, maior ou igual a zero, basta fazer o numerador da fração maior ou igual a zero:
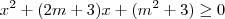
...
E proceder analogamente ao modo feito acima: achar as raízes, e pegar o intervalo entre elas (incluindo-as).
Por fim, basta fazer a interseção entre esses dois intervalos que você obteve.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por LuizAquino » Sáb Fev 26, 2011 20:49
por LuizAquino » Sáb Fev 26, 2011 20:49
Fabricio dalla escreveu:o conjunto de todos os valores de m para os quais a funçao
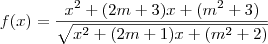
esta definida e é nao-negativa para todo x real é :
Para que essa função esteja definida, é necessário que
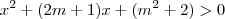
. Para que ela seja não negativa, é necessário que
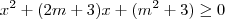
.
Estudando o sinal da parábola
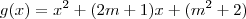
(que tem concavidade para cima), sabemos que ela será positiva quando:
- Se
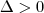 , para x<x' ou x>x''.
, para x<x' ou x>x''. - Se
 , para qualquer valor de x exceto x' (que é o mesmo que x'').
, para qualquer valor de x exceto x' (que é o mesmo que x''). - Se
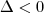 , para qualquer x.
, para qualquer x.
Onde temos que
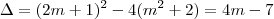
.
Para que g(x)>0 independente do valor de x, então devemos ter que
4m - 7 < 0, ou seja,
m < 7/4.
Estudando o sinal da parábola
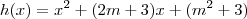
(que tem concavidade para cima), sabemos que ela será positiva ou nula quando:
- Se
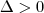 , para x<= x' ou x >= x''.
, para x<= x' ou x >= x''. - Se
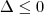 , para qualquer valor de x.
, para qualquer valor de x.
Onde temos que
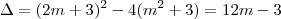
.
Para que h(x)>=0 independente do valor de x, então devemos ter que
12m - 3 <= 0, ou seja,
m <= 1/4.
Fazendo a interseção entre
m < 7/4 e
m <= 1/4, temos que
m <= 1/4.
Portanto, para
m <= 1/4, independente do valor real de x, a função está definida e é não-negativa.
Editado pela última vez por
LuizAquino em Sáb Fev 26, 2011 20:50, em um total de 1 vez.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Fabricio dalla » Sáb Fev 26, 2011 21:29
por Fabricio dalla » Sáb Fev 26, 2011 21:29
o valor do m de baixo e pra saber a condiçao de existencia do denominador da funçao
e o m de cima e pra saber o intervalo positivo de x?
obs:pra mim m tinha um valor soh :(
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Dom Fev 27, 2011 10:11
por LuizAquino » Dom Fev 27, 2011 10:11
Fabricio dalla escreveu:o valor do m de baixo é pra saber a condição de existência do denominador da função
e o m de cima e pra saber o intervalo positivo de x?
Sim.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5214 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
-
- [plano tangente a função de duas variaveis dada por função]
por isaac naruto » Qui Dez 31, 2015 16:35
- 0 Respostas
- 4339 Exibições
- Última mensagem por isaac naruto

Qui Dez 31, 2015 16:35
Cálculo: Limites, Derivadas e Integrais
-
- [Desigualdade] entre função exponencial e função potência
por VitorFN » Sex Mai 26, 2017 15:18
- 1 Respostas
- 5437 Exibições
- Última mensagem por adauto martins

Sex Jul 07, 2017 12:17
Álgebra Elementar
-
- +uma função das trevas.ajuda aew!(função par mas heim!?)
por Fabricio dalla » Dom Fev 27, 2011 16:12
- 2 Respostas
- 3337 Exibições
- Última mensagem por LuizAquino

Dom Mar 06, 2011 09:17
Funções
-
- [FUNÇÃO] Não consigo achar a fórmula da função
por LAZAROTTI » Qui Set 27, 2012 00:06
- 1 Respostas
- 2837 Exibições
- Última mensagem por MarceloFantini

Qui Set 27, 2012 07:13
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f(x)=\frac{{x}^{2}+(2m+3)x+({m}^{2}+3)}{\sqrt[2]{{x}^{2}+(2m+1)x+({m}^{2}+2)}} f(x)=\frac{{x}^{2}+(2m+3)x+({m}^{2}+3)}{\sqrt[2]{{x}^{2}+(2m+1)x+({m}^{2}+2)}}](/latexrender/pictures/1bd31fa69bc1c0007fb84f855ca01f35.png)

![f(x)=\frac{{x}^{2}+(2m+3)x+({m}^{2}+3)}{\sqrt[2]{{x}^{2}+(2m+1)x+({m}^{2}+2)}} f(x)=\frac{{x}^{2}+(2m+3)x+({m}^{2}+3)}{\sqrt[2]{{x}^{2}+(2m+1)x+({m}^{2}+2)}}](/latexrender/pictures/1bd31fa69bc1c0007fb84f855ca01f35.png)

![\sqrt[2]{{x}^{2}+(2m+1)x+({m}^{2}+2)}>0 \sqrt[2]{{x}^{2}+(2m+1)x+({m}^{2}+2)}>0](/latexrender/pictures/bc1981117145f4e3c4a4f251658bdb84.png)
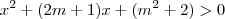
 é positivo, os valores maiores que zero desta equação será os valores entre as raízes.
é positivo, os valores maiores que zero desta equação será os valores entre as raízes.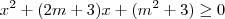


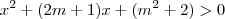 . Para que ela seja não negativa, é necessário que
. Para que ela seja não negativa, é necessário que 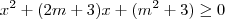 .
.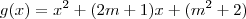 (que tem concavidade para cima), sabemos que ela será positiva quando:
(que tem concavidade para cima), sabemos que ela será positiva quando: , para x<x' ou x>x''.
, para x<x' ou x>x''. , para qualquer valor de x exceto x' (que é o mesmo que x'').
, para qualquer valor de x exceto x' (que é o mesmo que x''). , para qualquer x.
, para qualquer x.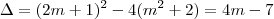 .
.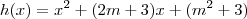 (que tem concavidade para cima), sabemos que ela será positiva ou nula quando:
(que tem concavidade para cima), sabemos que ela será positiva ou nula quando: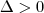 , para x<= x' ou x >= x''.
, para x<= x' ou x >= x''.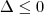 , para qualquer valor de x.
, para qualquer valor de x.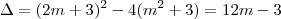 .
.




 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.