o conjunto de todos os valores de m para os quais a funçao
![f(x)=\frac{{x}^{2}+(2m+3)x+({m}^{2}+3)}{\sqrt[2]{{x}^{2}+(2m+1)x+({m}^{2}+2)}} f(x)=\frac{{x}^{2}+(2m+3)x+({m}^{2}+3)}{\sqrt[2]{{x}^{2}+(2m+1)x+({m}^{2}+2)}}](/latexrender/pictures/1bd31fa69bc1c0007fb84f855ca01f35.png)
esta definida e é nao-negativa para todo x real é :

![f(x)=\frac{{x}^{2}+(2m+3)x+({m}^{2}+3)}{\sqrt[2]{{x}^{2}+(2m+1)x+({m}^{2}+2)}} f(x)=\frac{{x}^{2}+(2m+3)x+({m}^{2}+3)}{\sqrt[2]{{x}^{2}+(2m+1)x+({m}^{2}+2)}}](/latexrender/pictures/1bd31fa69bc1c0007fb84f855ca01f35.png)

![\sqrt[2]{{x}^{2}+(2m+1)x+({m}^{2}+2)}>0 \sqrt[2]{{x}^{2}+(2m+1)x+({m}^{2}+2)}>0](/latexrender/pictures/bc1981117145f4e3c4a4f251658bdb84.png)
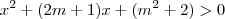
 é positivo, os valores maiores que zero desta equação será os valores entre as raízes.
é positivo, os valores maiores que zero desta equação será os valores entre as raízes.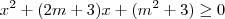


Fabricio dalla escreveu:o conjunto de todos os valores de m para os quais a funçao
esta definida e é nao-negativa para todo x real é :
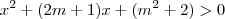 . Para que ela seja não negativa, é necessário que
. Para que ela seja não negativa, é necessário que 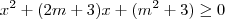 .
.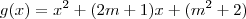 (que tem concavidade para cima), sabemos que ela será positiva quando:
(que tem concavidade para cima), sabemos que ela será positiva quando: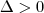 , para x<x' ou x>x''.
, para x<x' ou x>x''. , para qualquer valor de x exceto x' (que é o mesmo que x'').
, para qualquer valor de x exceto x' (que é o mesmo que x'').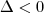 , para qualquer x.
, para qualquer x.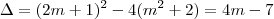 .
.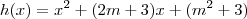 (que tem concavidade para cima), sabemos que ela será positiva ou nula quando:
(que tem concavidade para cima), sabemos que ela será positiva ou nula quando: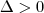 , para x<= x' ou x >= x''.
, para x<= x' ou x >= x''.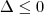 , para qualquer valor de x.
, para qualquer valor de x.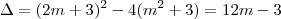 .
.

Fabricio dalla escreveu:o valor do m de baixo é pra saber a condição de existência do denominador da função
e o m de cima e pra saber o intervalo positivo de x?

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes