 por jmario » Qua Jun 09, 2010 09:01
por jmario » Qua Jun 09, 2010 09:01
As funções dipêndios são as seguintes:
![Dx(px,py,r)=\frac{r\sqrt[]{Px}}{\sqrt[]{Px}+\sqrt[]{Py}} Dx(px,py,r)=\frac{r\sqrt[]{Px}}{\sqrt[]{Px}+\sqrt[]{Py}}](/latexrender/pictures/36a66fef206b9437d9cce91685d3689e.png)
![Dy(px,py,r)=\frac{r\sqrt[]{Py}}{\sqrt[]{Px}+\sqrt[]{Py}} Dy(px,py,r)=\frac{r\sqrt[]{Py}}{\sqrt[]{Px}+\sqrt[]{Py}}](/latexrender/pictures/b6819fc7e51162b592bbcc9210e74346.png)
Por que a razão entre os dispêndios se transforma em:
![\frac{Dx(px,py,r}{Dy(px,py,r}=\frac{\sqrt[]{Px}}{\sqrt[]{Py}} \frac{Dx(px,py,r}{Dy(px,py,r}=\frac{\sqrt[]{Px}}{\sqrt[]{Py}}](/latexrender/pictures/fca2c327245a941f95bbbd6597a991f6.png)
Aí se calcula a derivada dessa razão com o
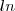
, não entendi porque usar o logarítmo natural na derivada
![\sigma=\frac{d ln\left[\frac{Dx(px,py,r)}{Dy(px,py,r)}\right]}{d ln \left(\frac{Px}{Py} \right)} \sigma=\frac{d ln\left[\frac{Dx(px,py,r)}{Dy(px,py,r)}\right]}{d ln \left(\frac{Px}{Py} \right)}](/latexrender/pictures/89c2c84b2bd9d0feac681d9126bfd88c.png)
Editado pela última vez por
jmario em Qua Jun 09, 2010 09:21, em um total de 1 vez.
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
 por jmario » Qua Jun 09, 2010 09:15
por jmario » Qua Jun 09, 2010 09:15
jmario escreveu:As funções dipêndios são as seguintes:
![Dx(px,py,r)=\frac{r\sqrt[]{Px}}{\sqrt[]{Px}+\sqrt[]{Py}} Dx(px,py,r)=\frac{r\sqrt[]{Px}}{\sqrt[]{Px}+\sqrt[]{Py}}](/latexrender/pictures/36a66fef206b9437d9cce91685d3689e.png)
![Dy(px,py,r)=\frac{r\sqrt[]{Py}}{\sqrt[]{Px}+\sqrt[]{Py}} Dy(px,py,r)=\frac{r\sqrt[]{Py}}{\sqrt[]{Px}+\sqrt[]{Py}}](/latexrender/pictures/b6819fc7e51162b592bbcc9210e74346.png)
Por que a razão entre os dispêndios se transforma em:
![\frac{Dx(px,py,r)}{Dy(px,py,r)}=\frac{\sqrt[]{Px}}{\sqrt[]{Py}} \frac{Dx(px,py,r)}{Dy(px,py,r)}=\frac{\sqrt[]{Px}}{\sqrt[]{Py}}](/latexrender/pictures/e86f0317335115d78c4523fa818441b2.png)
A fórmula da elasticidade de substituição é dada por:
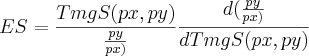
Aí se chega nessa equação com apenas a derivada dessa razão com o
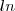
, não entendi porque usar o logarítmo natural na derivada
![\sigma=\frac{d ln\left[\frac{Dx(px,py,r)}{Dy(px,py,r)}\right]}{d ln \left(\frac{Px}{Py} \right)} \sigma=\frac{d ln\left[\frac{Dx(px,py,r)}{Dy(px,py,r)}\right]}{d ln \left(\frac{Px}{Py} \right)}](/latexrender/pictures/89c2c84b2bd9d0feac681d9126bfd88c.png)
Alguém pode me ajudar
Grato
José Mario
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
 por jmario » Qua Jun 09, 2010 09:22
por jmario » Qua Jun 09, 2010 09:22
jmario escreveu:jmario escreveu:As funções dipêndios são as seguintes:
![Dx(px,py,r)=\frac{r\sqrt[]{Px}}{\sqrt[]{Px}+\sqrt[]{Py}} Dx(px,py,r)=\frac{r\sqrt[]{Px}}{\sqrt[]{Px}+\sqrt[]{Py}}](/latexrender/pictures/36a66fef206b9437d9cce91685d3689e.png)
![Dy(px,py,r)=\frac{r\sqrt[]{Py}}{\sqrt[]{Px}+\sqrt[]{Py}} Dy(px,py,r)=\frac{r\sqrt[]{Py}}{\sqrt[]{Px}+\sqrt[]{Py}}](/latexrender/pictures/b6819fc7e51162b592bbcc9210e74346.png)
Por que a razão entre os dispêndios se transforma em:
![\frac{Dx(px,py,r)}{Dy(px,py,r)}=\frac{\sqrt[]{Px}}{\sqrt[]{Py}} \frac{Dx(px,py,r)}{Dy(px,py,r)}=\frac{\sqrt[]{Px}}{\sqrt[]{Py}}](/latexrender/pictures/e86f0317335115d78c4523fa818441b2.png)
A fórmula da elasticidade de substituição é dada por:
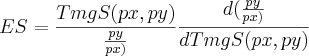
Aí se chega nessa equação com apenas a derivada dessa razão com o
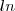
, não entendi porque usar o logarítmo natural na derivada
![\sigma=\frac{d ln\left[\frac{Dx(px,py,r)}{Dy(px,py,r)}\right]}{d ln \left(\frac{Px}{Py} \right)} \sigma=\frac{d ln\left[\frac{Dx(px,py,r)}{Dy(px,py,r)}\right]}{d ln \left(\frac{Px}{Py} \right)}](/latexrender/pictures/89c2c84b2bd9d0feac681d9126bfd88c.png)
Alguém pode me ajudar
Grato
José Mario
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
 por jmario » Qua Jun 09, 2010 09:23
por jmario » Qua Jun 09, 2010 09:23
jmario escreveu:jmario escreveu:As funções dipêndios são as seguintes:
![Dx(px,py,r)=\frac{r\sqrt[]{Px}}{\sqrt[]{Px}+\sqrt[]{Py}} Dx(px,py,r)=\frac{r\sqrt[]{Px}}{\sqrt[]{Px}+\sqrt[]{Py}}](/latexrender/pictures/36a66fef206b9437d9cce91685d3689e.png)
![Dy(px,py,r)=\frac{r\sqrt[]{Py}}{\sqrt[]{Px}+\sqrt[]{Py}} Dy(px,py,r)=\frac{r\sqrt[]{Py}}{\sqrt[]{Px}+\sqrt[]{Py}}](/latexrender/pictures/b6819fc7e51162b592bbcc9210e74346.png)
Por que a razão entre os dispêndios se transforma em:
![\frac{Dx(px,py,r)}{Dy(px,py,r)}=\frac{\sqrt[]{Px}}{\sqrt[]{Py}} \frac{Dx(px,py,r)}{Dy(px,py,r)}=\frac{\sqrt[]{Px}}{\sqrt[]{Py}}](/latexrender/pictures/e86f0317335115d78c4523fa818441b2.png)
A fórmula da elasticidade de substituição é dada por:
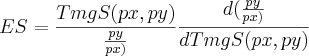
Aí se chega nessa equação com apenas a derivada dessa razão com o
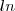
, não entendi porque usar o logarítmo natural na derivada
![\sigma=\frac{d ln\left[\frac{Dx(px,py,r)}{Dy(px,py,r)}\right]}{d ln \left(\frac{Px}{Py} \right)} \sigma=\frac{d ln\left[\frac{Dx(px,py,r)}{Dy(px,py,r)}\right]}{d ln \left(\frac{Px}{Py} \right)}](/latexrender/pictures/89c2c84b2bd9d0feac681d9126bfd88c.png)
Alguém pode me ajudar
Grato
José Mario
jmario escreveu:jmario escreveu:jmario escreveu:As funções dipêndios são as seguintes:
![Dx(px,py,r)=\frac{r\sqrt[]{Px}}{\sqrt[]{Px}+\sqrt[]{Py}} Dx(px,py,r)=\frac{r\sqrt[]{Px}}{\sqrt[]{Px}+\sqrt[]{Py}}](/latexrender/pictures/36a66fef206b9437d9cce91685d3689e.png)
![Dy(px,py,r)=\frac{r\sqrt[]{Py}}{\sqrt[]{Px}+\sqrt[]{Py}} Dy(px,py,r)=\frac{r\sqrt[]{Py}}{\sqrt[]{Px}+\sqrt[]{Py}}](/latexrender/pictures/b6819fc7e51162b592bbcc9210e74346.png)
Por que a razão entre os dispêndios se transforma em:
![\frac{Dx(px,py,r)}{Dy(px,py,r)}=\frac{\sqrt[]{Px}}{\sqrt[]{Py}} \frac{Dx(px,py,r)}{Dy(px,py,r)}=\frac{\sqrt[]{Px}}{\sqrt[]{Py}}](/latexrender/pictures/e86f0317335115d78c4523fa818441b2.png)
A fórmula da elasticidade de substituição é dada por:
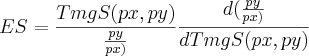
Aí se chega nessa equação com apenas a derivada dessa razão com o
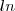
, não entendi porque usar o logarítmo natural na derivada
![\sigma=\frac{d ln\left[\frac{Dx(px,py,r)}{Dy(px,py,r)}\right]}{d ln \left(\frac{Px}{Py} \right)} \sigma=\frac{d ln\left[\frac{Dx(px,py,r)}{Dy(px,py,r)}\right]}{d ln \left(\frac{Px}{Py} \right)}](/latexrender/pictures/89c2c84b2bd9d0feac681d9126bfd88c.png)
Alguém pode me ajudar
Grato
José Mario
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
 por MarceloFantini » Qua Jun 09, 2010 20:59
por MarceloFantini » Qua Jun 09, 2010 20:59
José Mário,
não poste a mesma mensagem repetidas vezes em um curto intervalo de tempo. Isso ocupa muito espaço a troco de nada, não trará sua resposta mais rápido, é perda de tempo e é no mínimo não muito legal para com os outros.
Sobre a sua questão, quando você faz a razão
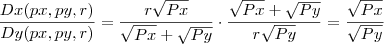
, os

cancelam-se e a mesma coisa com a soma das raízes.
E não sei porque derivar usando o logaritmo natural.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5584 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
-
- [plano tangente a função de duas variaveis dada por função]
por isaac naruto » Qui Dez 31, 2015 16:35
- 0 Respostas
- 4592 Exibições
- Última mensagem por isaac naruto

Qui Dez 31, 2015 16:35
Cálculo: Limites, Derivadas e Integrais
-
- [Desigualdade] entre função exponencial e função potência
por VitorFN » Sex Mai 26, 2017 15:18
- 1 Respostas
- 5751 Exibições
- Última mensagem por adauto martins

Sex Jul 07, 2017 12:17
Álgebra Elementar
-
- +uma função das trevas.ajuda aew!(função par mas heim!?)
por Fabricio dalla » Dom Fev 27, 2011 16:12
- 2 Respostas
- 3490 Exibições
- Última mensagem por LuizAquino

Dom Mar 06, 2011 09:17
Funções
-
- [FUNÇÃO] Não consigo achar a fórmula da função
por LAZAROTTI » Qui Set 27, 2012 00:06
- 1 Respostas
- 2958 Exibições
- Última mensagem por MarceloFantini

Qui Set 27, 2012 07:13
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![Dx(px,py,r)=\frac{r\sqrt[]{Px}}{\sqrt[]{Px}+\sqrt[]{Py}} Dx(px,py,r)=\frac{r\sqrt[]{Px}}{\sqrt[]{Px}+\sqrt[]{Py}}](/latexrender/pictures/36a66fef206b9437d9cce91685d3689e.png)
![Dy(px,py,r)=\frac{r\sqrt[]{Py}}{\sqrt[]{Px}+\sqrt[]{Py}} Dy(px,py,r)=\frac{r\sqrt[]{Py}}{\sqrt[]{Px}+\sqrt[]{Py}}](/latexrender/pictures/b6819fc7e51162b592bbcc9210e74346.png)
![\frac{Dx(px,py,r}{Dy(px,py,r}=\frac{\sqrt[]{Px}}{\sqrt[]{Py}} \frac{Dx(px,py,r}{Dy(px,py,r}=\frac{\sqrt[]{Px}}{\sqrt[]{Py}}](/latexrender/pictures/fca2c327245a941f95bbbd6597a991f6.png)
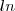 , não entendi porque usar o logarítmo natural na derivada
, não entendi porque usar o logarítmo natural na derivada![\sigma=\frac{d ln\left[\frac{Dx(px,py,r)}{Dy(px,py,r)}\right]}{d ln \left(\frac{Px}{Py} \right)} \sigma=\frac{d ln\left[\frac{Dx(px,py,r)}{Dy(px,py,r)}\right]}{d ln \left(\frac{Px}{Py} \right)}](/latexrender/pictures/89c2c84b2bd9d0feac681d9126bfd88c.png)

![Dx(px,py,r)=\frac{r\sqrt[]{Px}}{\sqrt[]{Px}+\sqrt[]{Py}} Dx(px,py,r)=\frac{r\sqrt[]{Px}}{\sqrt[]{Px}+\sqrt[]{Py}}](/latexrender/pictures/36a66fef206b9437d9cce91685d3689e.png)
![Dy(px,py,r)=\frac{r\sqrt[]{Py}}{\sqrt[]{Px}+\sqrt[]{Py}} Dy(px,py,r)=\frac{r\sqrt[]{Py}}{\sqrt[]{Px}+\sqrt[]{Py}}](/latexrender/pictures/b6819fc7e51162b592bbcc9210e74346.png)
![\frac{Dx(px,py,r}{Dy(px,py,r}=\frac{\sqrt[]{Px}}{\sqrt[]{Py}} \frac{Dx(px,py,r}{Dy(px,py,r}=\frac{\sqrt[]{Px}}{\sqrt[]{Py}}](/latexrender/pictures/fca2c327245a941f95bbbd6597a991f6.png)
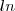 , não entendi porque usar o logarítmo natural na derivada
, não entendi porque usar o logarítmo natural na derivada![\sigma=\frac{d ln\left[\frac{Dx(px,py,r)}{Dy(px,py,r)}\right]}{d ln \left(\frac{Px}{Py} \right)} \sigma=\frac{d ln\left[\frac{Dx(px,py,r)}{Dy(px,py,r)}\right]}{d ln \left(\frac{Px}{Py} \right)}](/latexrender/pictures/89c2c84b2bd9d0feac681d9126bfd88c.png)

, não entendi porque usar o logarítmo natural na derivada

, não entendi porque usar o logarítmo natural na derivada

, não entendi porque usar o logarítmo natural na derivada
, não entendi porque usar o logarítmo natural na derivada

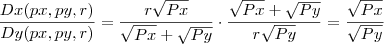 , os
, os  cancelam-se e a mesma coisa com a soma das raízes.
cancelam-se e a mesma coisa com a soma das raízes.

