 por jmario » Ter Mai 18, 2010 09:13
por jmario » Ter Mai 18, 2010 09:13
Dado o seguinte lambda
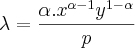
A restrição orçamentária é dada por
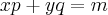
Substituindo a função de demanda de
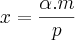
e a função demanda
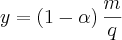
Substituindo essas duas funções demandas no lambda abaixo
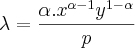
, fica assim:
![\lambda=\frac{\alpha\left(\frac{\alpha.m}{p}\right)^{\alpha-1}\left[\left(1-\alpha \right)\frac{m}{q} \right]^{1-\alpha}}{p} \lambda=\frac{\alpha\left(\frac{\alpha.m}{p}\right)^{\alpha-1}\left[\left(1-\alpha \right)\frac{m}{q} \right]^{1-\alpha}}{p}](/latexrender/pictures/4cbff281ef10718ff4083380edadea0a.png)
O resultado é esse
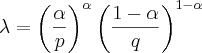
O problema é que eu não sei como se chega nessa solução.
Grato
José Mario
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
 por MarceloFantini » Ter Mai 18, 2010 19:59
por MarceloFantini » Ter Mai 18, 2010 19:59
Continuando após a sua última linha, vou aplicar as potências:
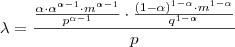
No m, some as potências
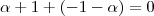
, no

também:

, e finalmente no p:

, resultando em:
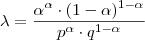
Agrupando:
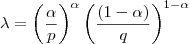
Qualquer dúvida comente.
P.S.: Cacete, meu LaTeX por algum motivo fica pequeno. -_-
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- isolamento de função lagrangeana
por jmario » Qui Mai 13, 2010 08:41
- 7 Respostas
- 3958 Exibições
- Última mensagem por MarceloFantini

Ter Mai 18, 2010 19:33
Funções
-
- isolamento de equação
por jmario » Seg Mai 10, 2010 12:39
- 6 Respostas
- 3069 Exibições
- Última mensagem por jmario

Ter Mai 11, 2010 16:03
Funções
-
- isolamento de variável
por jmario » Sex Jun 04, 2010 08:39
- 3 Respostas
- 3705 Exibições
- Última mensagem por Mathmatematica

Sáb Jun 05, 2010 13:02
Álgebra Elementar
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5580 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
-
- [plano tangente a função de duas variaveis dada por função]
por isaac naruto » Qui Dez 31, 2015 16:35
- 0 Respostas
- 4592 Exibições
- Última mensagem por isaac naruto

Qui Dez 31, 2015 16:35
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
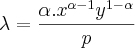
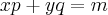
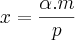 e a função demanda
e a função demanda 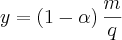
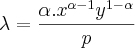 , fica assim:
, fica assim:![\lambda=\frac{\alpha\left(\frac{\alpha.m}{p}\right)^{\alpha-1}\left[\left(1-\alpha \right)\frac{m}{q} \right]^{1-\alpha}}{p} \lambda=\frac{\alpha\left(\frac{\alpha.m}{p}\right)^{\alpha-1}\left[\left(1-\alpha \right)\frac{m}{q} \right]^{1-\alpha}}{p}](/latexrender/pictures/4cbff281ef10718ff4083380edadea0a.png)
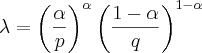


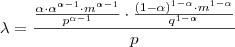
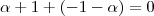 , no
, no  também:
também:  , e finalmente no p:
, e finalmente no p:  , resultando em:
, resultando em: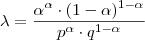
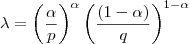



 .
.
 :
: