 por jmario » Seg Mai 10, 2010 12:39
por jmario » Seg Mai 10, 2010 12:39
Eu tenho a seguinte equação
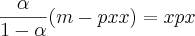
isolando o pxx fica
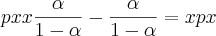
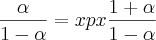
eu não se se fica assim, aí começa a minha dúvida
Como se resolve essa equação?
Eu só sei que a resposta correta no final é
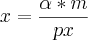
Como se faz para chegar nesse resultado
Grato
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
 por Douglasm » Ter Mai 11, 2010 13:10
por Douglasm » Ter Mai 11, 2010 13:10
Olá jmario. Eu não sei se essa é a mesma que a última que você postou, mas o resultado é o mesmo. Antes de responder, só uma pergunta: Quando você escreve
"pxx" você quer dizer
"p . x . x = p . x²" ou
"P(x).x"?. Eu considerei que se tratava da segunda opção:
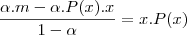
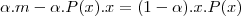
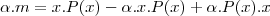
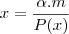
Acredito que seja só isso. Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por jmario » Ter Mai 11, 2010 13:34
por jmario » Ter Mai 11, 2010 13:34
Oi Douglas
MAS EU FIQUEI COM UM DÚVIDA: O QUE VOCÊ FEZ COM O 1 DO

O QUE VOCÊ FEZ COM O 1
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
 por jmario » Ter Mai 11, 2010 13:50
por jmario » Ter Mai 11, 2010 13:50
Mas isso não entrou na equação
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
 por Douglasm » Ter Mai 11, 2010 15:22
por Douglasm » Ter Mai 11, 2010 15:22
Entrou sim, na terceira linha. Veja que foi feito esse produto, ao mesmo tempo que "passei" o "
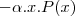
" para o outro lado da equação, em que ele se torna "
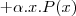
".
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por jmario » Ter Mai 11, 2010 16:03
por jmario » Ter Mai 11, 2010 16:03
Tá certo muito obrigado
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- isolamento de função
por jmario » Ter Mai 18, 2010 09:13
- 1 Respostas
- 1252 Exibições
- Última mensagem por MarceloFantini

Ter Mai 18, 2010 19:59
Funções
-
- isolamento de variável
por jmario » Sex Jun 04, 2010 08:39
- 3 Respostas
- 3702 Exibições
- Última mensagem por Mathmatematica

Sáb Jun 05, 2010 13:02
Álgebra Elementar
-
- isolamento de função lagrangeana
por jmario » Qui Mai 13, 2010 08:41
- 7 Respostas
- 3956 Exibições
- Última mensagem por MarceloFantini

Ter Mai 18, 2010 19:33
Funções
-
- Equação - Dúvida básica sobre a proporcionalidade de equação
por FelipeGM » Qui Jan 12, 2012 19:05
- 4 Respostas
- 7731 Exibições
- Última mensagem por FelipeGM

Sáb Jan 14, 2012 13:16
Álgebra Elementar
-
- Equação - como montar a equação desse problema?
por _Manu » Qua Jul 04, 2012 03:37
- 7 Respostas
- 13237 Exibições
- Última mensagem por _Manu

Qui Jul 05, 2012 01:49
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
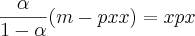
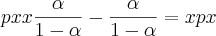
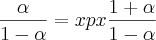 eu não se se fica assim, aí começa a minha dúvida
eu não se se fica assim, aí começa a minha dúvida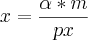

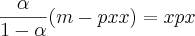
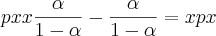
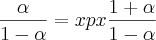 eu não se se fica assim, aí começa a minha dúvida
eu não se se fica assim, aí começa a minha dúvida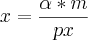

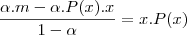
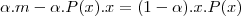
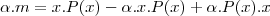
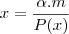





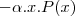 " para o outro lado da equação, em que ele se torna "
" para o outro lado da equação, em que ele se torna "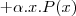 ".
".



 , avisa que eu resolvo.
, avisa que eu resolvo.

