Considere a função
![f:[0, 5]\rightarrow R f:[0, 5]\rightarrow R](/latexrender/pictures/5b6d697b97198c3fa54ebc05dcbb2cde.png) cujo gráfico está representado na figura a seguir:
cujo gráfico está representado na figura a seguir:Assinale a alternativa que melhor representa o gráfico da função da área delimitada pelo gráfico da função f e o eixo da abscissa, no intervalo
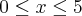 :
:
![f:[0, 5]\rightarrow R f:[0, 5]\rightarrow R](/latexrender/pictures/5b6d697b97198c3fa54ebc05dcbb2cde.png) cujo gráfico está representado na figura a seguir:
cujo gráfico está representado na figura a seguir: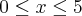 :
:
![f: [0,5] \mapsto \mathbb{R} f: [0,5] \mapsto \mathbb{R}](/latexrender/pictures/e8b1cb52eeb0ca24fd56ccc1a79e8f0d.png) , a saber
, a saber ![f(x) = \begin{cases} 2x ; x \in [0,1] \\ 2 ; x \in (1,2) \\ 1/2 ; x \in [2,4) \\ -2x + 10 ; x \in (4,5] \end{cases} f(x) = \begin{cases} 2x ; x \in [0,1] \\ 2 ; x \in (1,2) \\ 1/2 ; x \in [2,4) \\ -2x + 10 ; x \in (4,5] \end{cases}](/latexrender/pictures/a455e8b5b3d453c7fe9fb32267676c37.png) .
.![x \in [0,1] , x \in (1,2) , x \in [2,4) , x \in (4,5] x \in [0,1] , x \in (1,2) , x \in [2,4) , x \in (4,5]](/latexrender/pictures/278b1a153759caeaeec9821c655b2fc3.png) .
.  e altura
e altura 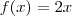 ; no segundo caso , terá de calcular área de um retângulo de lados
; no segundo caso , terá de calcular área de um retângulo de lados  e
e  ; no terceiro deve calcular a área de um retângulo de lados
; no terceiro deve calcular a área de um retângulo de lados  e
e 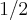 ; no último caso , conforme no 1° , deve computar a área de um triângulo retângulo de mesma altura do primeiro ,porém bases distintas (em geral) que és 5 - x [/tex] .
; no último caso , conforme no 1° , deve computar a área de um triângulo retângulo de mesma altura do primeiro ,porém bases distintas (em geral) que és 5 - x [/tex] .  , definida do conjunto
, definida do conjunto ![[0,5] [0,5]](/latexrender/pictures/be66a98c7ffb0b7cd18378674ce90c9c.png) ao
ao  .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

