funcao

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

funcao

Regras do fórum
Responder

funcao

Mensagempor renan oliveira » Dom Out 06, 2013 16:48

Não me lembro mais como se resolve esse tipo de questão.
Qual é o valor de p para o qual os pontos (3p, 2p), (4, 1) e (2, 3) são colineares?

(A) -1
(B) 0
(C) 1
(D) 2
(E) 3
renan oliveira
Novo Usuário
Novo Usuário
 
Mensagens: 1
Registrado em: Dom Out 06, 2013 16:33
Formação Escolar: ENSINO MÉDIO
Área/Curso: exata
Andamento: formado
Voltar ao topo

Re: funcao

Mensagempor zaspers » Ter Out 08, 2013 07:18

Creio que a resposta seja a seguinte:

(1) monte uma matriz
\begin{pmatrix} 3p & 2p & 1 \\ 4 & 1 & 1 \\ 2 & 3 & 1 \end{pmatrix}

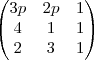
(2) como resolução teremos:
3p+4p+12 = -9p-2p-2

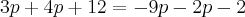
(3) resolvendo o resultado será
-1
zaspers
Novo Usuário
Novo Usuário
 
Mensagens: 3
Registrado em: Ter Out 08, 2013 06:54
Formação Escolar: GRADUAÇÃO
Área/Curso: Eng. Elétrica
Andamento: cursando
Voltar ao topo

Re: funcao

Mensagempor Bravim » Qui Out 10, 2013 01:40

Olha... eu acho que você se enganou... http://www.wolframalpha.com/share/clip?f=d41d8cd98f00b204e9800998ecf8427el7srlp5veb
O resultado certo é,
1=4a+b
3=2a+b
Daqui encontramos que b=5, a=-1
e daí substituimos em:
2p=-3p+5
p=1
Com o ponto (3,2), (que por coincidência é o ponto médio do segmento!)
Imagem
Avatar do usuário
Bravim
Usuário Parceiro
Usuário Parceiro
 
Mensagens: 57
Registrado em: Qui Out 03, 2013 03:28
Formação Escolar: GRADUAÇÃO
Área/Curso: Engenharia
Andamento: cursando
Voltar ao topo
Responder

Voltar para Funções

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes

 


Tópico Popular

Assunto: Exercicios de polinomios
Autor: shaft - Qua Jun 30, 2010 17:30

2x+5=\left(x+m\right)²-\left(x-n \right)²

Então, o exercicio pede para encontrar {m}^{3}-{n}^{3}.

Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !

Assunto: Exercicios de polinomios
Autor: Douglasm - Qua Jun 30, 2010 17:53

Bom, se desenvolvermos isso, encontramos:

2x+5 = 2x(m+n) + m^2-n^2

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):

2(m+n) = 2 \;\therefore\; m+n = 1

m^2-n^2 = 5 \;\therefore\; (m+n)(m-n) = 5 \;\therefore\; (m-n) = 5

Somando a primeira e a segunda equação:

2m = 6 \;\therefore\; m = 3 \;\mbox{consequentemente:}\; n=-2

Finalmente:

m^3 - n^3 = 27 + 8 = 35

Até a próxima.

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

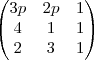
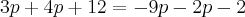
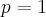
Índice do fórum