Esse exercicio como é :determine o(s) zero(s) ou a(s) raiz(es) das seguintes funçoes quadraticas:
f(x)=xelevado a 2-4, f(x)=xelevado a 2+2x, f(x)=xelevado a 2-6x+9, f(x)=xelevado a 2-10x+16 ...
por Fiel8 » Qua Jul 01, 2009 17:29
por Molina » Qua Jul 01, 2009 20:49
por Cleyson007 » Sex Jul 03, 2009 12:19
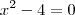
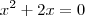
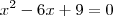
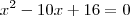
, faça o seguinte: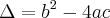 
.![\frac{-b{+}_{-}\sqrt[2]{\Delta}}{2a}](/latexrender/pictures/a5f899a48af422cd544594f88cab7fcd.png "\frac{-b{+}_{-}\sqrt[2]{\Delta}}{2a}")
. 
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será , mas negativo pois tem de ser no quarto quadrante. Se 
, então 
. Como módulo é um: 
.
.