 por Thauan_Barcellos » Sex Out 14, 2011 16:27
por Thauan_Barcellos » Sex Out 14, 2011 16:27
Olá pessoal , estava fazendo esta questão :
(UFMG) Seja
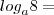
-

, a>0 . O Valor da base a é :
a) 1/16
b) 1/8
c )2
d)10
e)16
Bom inicialmente eu tentei fazer isso :
a -

=8
1 -

= 8
Como que devo começar a fazer esta equação ?
-
Thauan_Barcellos
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Ago 20, 2011 11:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por TheoFerraz » Sex Out 14, 2011 16:58
por TheoFerraz » Sex Out 14, 2011 16:58
Sempre que voce estiver lidando com logarítimos, ao ver o seguinte termo matematico :
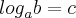
Leia em voz alta da seguinte forma: "Qual número 'c' que eu devo elevar a base 'a' de modo a resultar em 'b'
entao no seu caso:
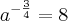
Pelas regras de potenciação:
![\frac{1}{\sqrt[4]{{a}^{3}}} = 8 \frac{1}{\sqrt[4]{{a}^{3}}} = 8](/latexrender/pictures/f0cde939070b58e0b239c197664615d4.png)
![\sqrt[4]{{a}^{3}} = \frac{1}{8} \sqrt[4]{{a}^{3}} = \frac{1}{8}](/latexrender/pictures/4fe474e926bcad56dfbccf717f7a6f59.png)
ou melhor
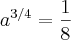
preferi escrever assim pq agora pra passar para o outro lado ficaria :
![a = {\left(\frac{1}{8} \right)}^{4/3} = \sqrt[3]{{\left(\frac{1}{8} \right)}^{4}} = \sqrt[3]{\frac{1}{4096}} = \frac{1}{16} a = {\left(\frac{1}{8} \right)}^{4/3} = \sqrt[3]{{\left(\frac{1}{8} \right)}^{4}} = \sqrt[3]{\frac{1}{4096}} = \frac{1}{16}](/latexrender/pictures/51be3713e6e94656a16bb48e4fc57a70.png)
Simples assim.
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por Thauan_Barcellos » Sex Out 14, 2011 17:08
por Thauan_Barcellos » Sex Out 14, 2011 17:08
Dúvida respondida , obrigado pela ajuda

-
Thauan_Barcellos
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Ago 20, 2011 11:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função Logarítmica
por OtavioBonassi » Qui Jan 06, 2011 21:58
- 12 Respostas
- 8042 Exibições
- Última mensagem por OtavioBonassi

Sex Jan 07, 2011 23:42
Funções
-
- Função Logaritmica
por nessitahfl » Qui Abr 17, 2014 11:06
- 3 Respostas
- 2586 Exibições
- Última mensagem por nessitahfl

Ter Abr 22, 2014 10:48
Funções
-
- Função Logarítmica
por Carlos28 » Sex Mar 13, 2015 10:02
- 2 Respostas
- 2471 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:36
Logaritmos
-
- Função logarítmica
por zenildo » Qua Jul 15, 2015 12:26
- 1 Respostas
- 2058 Exibições
- Última mensagem por nakagumahissao

Qui Jul 16, 2015 14:37
Logaritmos
-
- Função Logarítmica - Urgente!
por Asustek27 » Dom Mar 14, 2010 19:24
- 2 Respostas
- 2688 Exibições
- Última mensagem por Asustek27

Seg Mar 15, 2010 15:25
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
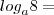 -
- , a>0 . O Valor da base a é :
, a>0 . O Valor da base a é : =8
=8 = 8
= 8
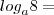 -
- , a>0 . O Valor da base a é :
, a>0 . O Valor da base a é : =8
=8 = 8
= 8
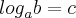
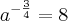
![\frac{1}{\sqrt[4]{{a}^{3}}} = 8 \frac{1}{\sqrt[4]{{a}^{3}}} = 8](/latexrender/pictures/f0cde939070b58e0b239c197664615d4.png)
![\sqrt[4]{{a}^{3}} = \frac{1}{8} \sqrt[4]{{a}^{3}} = \frac{1}{8}](/latexrender/pictures/4fe474e926bcad56dfbccf717f7a6f59.png) ou melhor
ou melhor 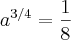
![a = {\left(\frac{1}{8} \right)}^{4/3} = \sqrt[3]{{\left(\frac{1}{8} \right)}^{4}} = \sqrt[3]{\frac{1}{4096}} = \frac{1}{16} a = {\left(\frac{1}{8} \right)}^{4/3} = \sqrt[3]{{\left(\frac{1}{8} \right)}^{4}} = \sqrt[3]{\frac{1}{4096}} = \frac{1}{16}](/latexrender/pictures/51be3713e6e94656a16bb48e4fc57a70.png)








