 por Kelvin Brayan » Ter Mai 24, 2011 16:21
por Kelvin Brayan » Ter Mai 24, 2011 16:21
O que é ponto de inflexão? esse ponto sempre coincide com o zero ou raiz da função?
-
Kelvin Brayan
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
 por norberto » Ter Mai 24, 2011 17:19
por norberto » Ter Mai 24, 2011 17:19
Oi Kelvin !
Kelvin escreveu:O que é ponto de inflexão?
Pontos de inflexão, são os pontos em que a concavidade da curva muda.
Kelvin escreveu:esse ponto sempre coincide com o zero ou raiz da função?
Não. Na verdade, eles coincidem coma as raízes da segunda derivada da função.
Por exemplo :

A primeira derivada é :

E a segunda derivada é :

É fácil ver que 0 é a raiz dessa equação.
Portanto 0 é um ponto de inflexão de

Abraços.
Editado pela última vez por
norberto em Ter Mai 24, 2011 17:54, em um total de 1 vez.
-
norberto
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Qua Mai 18, 2011 04:38
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Kelvin Brayan » Ter Mai 24, 2011 17:29
por Kelvin Brayan » Ter Mai 24, 2011 17:29
Valeu!
-
Kelvin Brayan
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
 por Fabio Cabral » Ter Jun 07, 2011 13:29
por Fabio Cabral » Ter Jun 07, 2011 13:29
O ponto de inflexão é dado pela raíz da segunda derivada

.
Ou seja, igualar
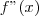
a 0.
Nesse caso, o ponto de inflexão não seria

?
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Ponto Crítico e Ponto de Inflexão e intervalos] Dúvidas em
por Andre Lopes » Qua Set 26, 2012 00:37
- 2 Respostas
- 3384 Exibições
- Última mensagem por MarceloFantini

Qui Set 27, 2012 06:56
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo I] Concavidade - Ponto de Inflexão
por Pessoa Estranha » Ter Nov 18, 2014 00:38
- 3 Respostas
- 2405 Exibições
- Última mensagem por adauto martins

Sex Nov 21, 2014 17:01
Cálculo: Limites, Derivadas e Integrais
-
- [AJUDA] Derivada: Ponto Máx, Minimo, Inflexão e Assíntota
por Mateus Leao » Qua Mai 16, 2012 13:03
- 2 Respostas
- 2392 Exibições
- Última mensagem por ricardosanto

Sex Mai 18, 2012 19:36
Cálculo: Limites, Derivadas e Integrais
-
- ponto da reta r que é eqüidistante do ponto A e do ponto B
por gutorocher » Qua Jul 21, 2010 14:01
- 12 Respostas
- 15170 Exibições
- Última mensagem por gutorocher

Sex Jul 23, 2010 13:04
Geometria Analítica
-
- [Vetores] Ponto de reta próximo a outros pares de ponto
por cmcrz97 » Ter Jun 19, 2018 20:29
- 0 Respostas
- 2915 Exibições
- Última mensagem por cmcrz97

Ter Jun 19, 2018 20:29
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.









 .
.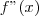 a 0.
a 0. ?
?

 .
.



