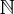 . No entanto surgiu-me uma dúvida.
. No entanto surgiu-me uma dúvida.Será o conjunto dos inteiros não nulos {1,2,3,4,5,6,7....} ou dos inteiros não negativos
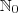 , {0,1,2,3,4,5,6,7....}.
, {0,1,2,3,4,5,6,7....}.Nos livros que utilizo o 0 não entra nos
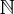 , mas na internet encontrei uma abordagem as sequências com base nos
, mas na internet encontrei uma abordagem as sequências com base nos 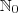 .Pode parecer um promenor, mas não é!
.Pode parecer um promenor, mas não é!Imaginemos a sucessão
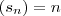 . Se o dominio for
. Se o dominio for 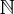 temos que o primeiro termo é 1, se o dominio for
temos que o primeiro termo é 1, se o dominio for 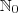 , o primeiro termo é 0.
, o primeiro termo é 0.Existe alguma convenção?
Normalmente qual o conjunto que utilizam para o estudo das sequências?





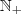 .
.
 para representar o conjunto dos naturais sem o zero.
para representar o conjunto dos naturais sem o zero.
 , avisa que eu resolvo.
, avisa que eu resolvo.

