Sejam a, b ,c números reais positivos distintos dois a dois tais que a² + b² - ab = c² .
Prove que o produto ( a - c )( b - c ) é negativo



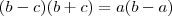
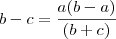

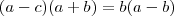
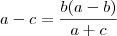
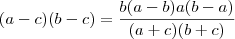
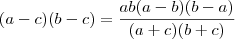

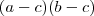 é positivo ,isto é ,
é positivo ,isto é , 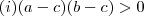 .
.  ocorrerá
ocorrerá 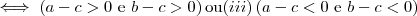
 .Deixando
.Deixando  em evidência e somando-se
em evidência e somando-se 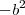 em ambos membros ,obtemos que
em ambos membros ,obtemos que 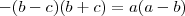 .Como
.Como 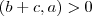 ,decorre que (iv)
,decorre que (iv) e
e 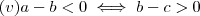 .Além disso ,pela suposição do produto ser positivo ,segue
.Além disso ,pela suposição do produto ser positivo ,segue 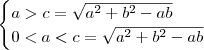 .
. 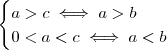 .
.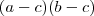 é negativo .
é negativo .
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)