Estudante13,
Resolução:
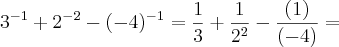

Tirando o Mínimo Múltiplo Comum entre os denominadores 3, 4 e 4, tem-se que:
3 4 4 | 2
3 2 2 | 2
3 1 1 | 3
1 1 1 |
Primeiro, tenta-se dividir 3, 4 e 4 por 2. Como somente os dois números quatro são divisíveis por 2, repete-se na segunda linha o 3, e 4/2 = 2 embaixo dos dois números quatro. Como ainda dá para continuar dividindo por 2, coloca-se o segundo número 2 à direita da barra e divide-se 3, 2 e 2 por 2, ficando 3, 1 e 1. Como somente sobrou o 3 e o único número que divide o 3 é ele mesmo, coloca-se o três à direita da barra e divide-se 3, 1 e 1 por 3, ficando com 1, 1, 1 finalmente. Chegando neste ponto, ou seja, 1, 1 e 1, temos o resultado do MMC (Mínimo Múltiplo Comum), que nada mais é que o a multiplicação dos divisores encontrados, que neste caso são: 2, 2 e 3 e que se encontram à direita da barra.
Multiplicando-os, teremos: 2 x 2 x 3 = 12
Assim, o 12 irá para o denominador. Por fim, toma-se o 12 encontrado e divide-se por cada denominador e multiplica-se pelo numerador. Por exemplo: Para 1/3, pega-se o 12, divide-se por 3 e multiplica-se por 1, ficando 4/3. Faça isto para as três frações acima. Desta maneira, tudo ficará da seguinte forma:
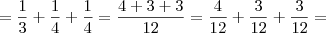
Que nada mais é do que:
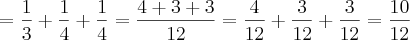
Que por sua vez, dividindo-se o numerador por 2 e o denominador por 2, ficará:
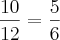
Espero ter sanado sua dúvida.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali



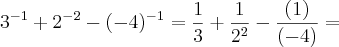

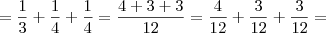
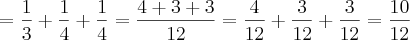
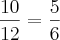


 .
.
 :
: