Sabemos que num triângulo retângulo é verdadeiro que a soma das áreas dos catetos é igual a área da hipotenusa.
Isto é:
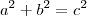
Agora, adicionando o conceito de unidade a esta fórmula, como ficaria?
Assim?
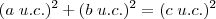 sendo:
sendo: 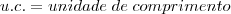
Ou assim?
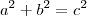
Sendo:
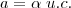
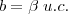
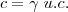
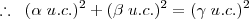
Bem, o que eu busco saber com essa pergunta!? Em 1º lugar, buscar um padrão para as situações semelhantes, é isso o que fazemos em ciencias exatas, buscamos regras gerais e padrões, e em 2º lugar, na álgebra, existe um elemento para representar uma grandeza, um elemento para representar uma unidade e um elemento para representar o coeficiente desta unidade, então, quero fazer um cara-crachá nas fórmulas matemáticas.
Grato!


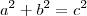
 são em COMPRIMENTO, ou seja, a = 10cm, a = 20dm, a = 10m, a = 12km, etc.
são em COMPRIMENTO, ou seja, a = 10cm, a = 20dm, a = 10m, a = 12km, etc.  também estão em comprimento,
também estão em comprimento, 
 e
e  são grandezas de comprimento. Você decide como expor a unidade da grandeza!
são grandezas de comprimento. Você decide como expor a unidade da grandeza!  [L].
[L].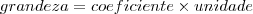
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.