z = (x,y)
 =-1
=-1i=(0,1)
então....(0,1)(0,1) = (0-1,0+0) = (-1,0)
z = (x=-1,y=0) = (-1,0)
onde x é a parte real de z e y a parte imaginária de z
está certo?
então o
 =x eu posso dizer de acordo com isso que
=x eu posso dizer de acordo com isso que  ou -1 é a parte real de z?
ou -1 é a parte real de z?OBRIGADO

 =-1
=-1 =x eu posso dizer de acordo com isso que
=x eu posso dizer de acordo com isso que  ou -1 é a parte real de z?
ou -1 é a parte real de z?

![\sqrt[]{-1} \sqrt[]{-1}](/latexrender/pictures/96dee42b6f915f610697937e8c654c44.png)

lieberth escreveu:
mas pode mudar as letras? ex: a+bi
poderia ser x+yi?
A=X E B=Y
o i no meu livro está i= (0,1) esse i é o mesmo que



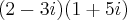
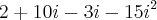 -->
--> 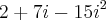 --> Lembrando que
--> Lembrando que 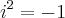

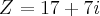


lieberth escreveu:olha essa:
certo essa?


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)