Dúvida em subtração de números inteiros

[LuizCarlos]

Olá amigos professores.

Estou resolvendo exercícios e problemas que envolvem subtração de números inteiros, mas não estou conseguindo entender a ideia de diferença entre números inteiros, está confuso.
Consigo entender a Adição de números inteiros, pensando da seguinte forma, sinal negativo é dívida, e sinal positivo é o que tenho para pagar a dívida, pensando assim, fica fácil de entender, porém com a subtração de números inteiros, não consigo entender pensando da mesma forma, como se fosse dívida e o que tenho para pagar essa dívida.

Entendi que na adição de números inteiros, assim como na multiplicação, existem propriedades, e na subtração e divisão não existe.
Entendi também que a ordem dos valores na subtração, altera a diferença(resultado), já na adição a ordem das parcelas não altera a soma (propriedade comutativa).

Consigo resolver contas como por exemplo:


Mas tentei resolver esse problema e não consegui, por falta de enteder o conceito de diferença entre números inteiros.

Durante uma viagem interplanetária a temperatura externa á nave diminuiu de 908 graus para -684 graus, num certo período.
Responda:
a) Qual é a subtração de números inteiros que representa essa variação de temperatura.

b) De quantos graus é a diferença. Use um número inteiro para dar a resposta.

Tentando resolver, fiz dessa forma:


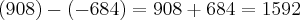
Mas vi a resposta atrás do livro, está

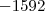
Levando em consideração a ordem da diferença:



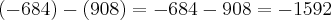
Mas não estou entendendo porque a conta não deve ser feita levando em consideração a ordem

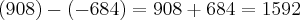
Não estou entendendo, estou confuso.

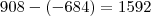
[fraol]

Suponho que o livro esteja considerando que a reposta deva se referir a qual foi a variação. Nesse caso como a temperatura caiu, houve uma variação negativa.

Quanto à diferença entre os números, a sua conta está correta:

Quanto à considerar o sinal de negativo como "dívida" é uma analogia que serve em muitos casos, mas pode gerar confusão em alguns outros.