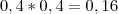NMiguel escreveu:Sabemos que os dois lançamentos são independentes, isto é, o resultado do primeiro lançamento não influencia o segundo. Assim, se queremos a probabilidade nunca sair cara, basta multiplicarmos a probabilidade de não sair cara no primeiro lançamento pela probabilidade de não sair cara no segundo lançamento, isto é,
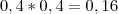


obrigado meu brother,
dai, como a probabilidade de 0,6 dando cara implica em uma moeda "hakeada", se acrescentarmos uma moeda honesta
(probabilidade de dar cara = 0,5), ficamos com duas moedas - uma hakeada e outra boa, pois bem, se selecionamos uma moeda
aleatóriamente isso nos daria a mesma probabilidade de 0,5, porque temos duas moedas, dai se lançarmos uma duas vezes e nas duas vezes dá cara.
Qual seria a probabilidade de termos pegado a moeda "hakeada"?
cara, é que to fazendo um curso on line que é muito rápido, eu ate q tenho vontade para estudar sim, mas cairam tres questoes sobre probabilidade, a primeira eu sabia, que era: 'se temos uma moeda com 0,6 de chance de dar cara, qual seria a chance de dar coroa" essa eu acertei que é obvia, 0,4, mas as outras duas seguintes que uma é essa q vc me ajudou e a outra, essa que to postando complicou e pra complicar mais, o curso é em ingles...
obrigado