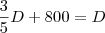por paulo nieres » Seg Fev 27, 2012 14:30
por paulo nieres » Seg Fev 27, 2012 14:30
OLá tudo bem eu acabei de entrar na faculdade ai essa semana fui fazer uma revisão nos meu conhecimentos de matematica ai encontrei um problema que não consegui resolver até agora e queria ajuda de vocês, o problema e esse:
Eu tenho uma divida de D reais no 1° mês paguei 1/4 do total da divida e 1/5 do que restou no 2° mês, e no 3° mes paguei a terça parte do que restou e finalizei a divida com um pagamento de R$:800,00 qual era o valor de D?
-
paulo nieres
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Fev 27, 2012 14:14
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Florestal
- Andamento: cursando
 por LuizAquino » Seg Fev 27, 2012 22:53
por LuizAquino » Seg Fev 27, 2012 22:53
paulo nieres escreveu:Eu tenho uma divida de D reais no 1° mês paguei 1/4 do total da divida e 1/5 do que restou no 2° mês, e no 3° mes paguei a terça parte do que restou e finalizei a divida com um pagamento de R$:800,00 qual era o valor de D?
No 1º mês, foi pago
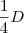
. Sobrou então
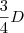
.
No 2º mês, foi pago 1/5 do que restou em relação ao 1º mês. Desse modo, foi pago
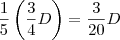
.
Até agora, já foi pago
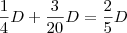
. Sobrou então
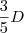
.
No 3º mês, foi pago 1/3 do que restou em relação ao 2º mês. Desse modo, foi pago
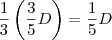
.
Até agora, já foi pago
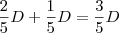
.
Por fim, a dívida foi finalizada com um pagamento de R$ 800,00.
Desse modo, somando
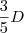
com R$ 800,00 obtemos o valor da dívida.
Temos então que:
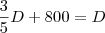
Resolvendo essa equação, obtemos que a dívida é igual a R$ 2.000,00.
paulo nieres escreveu:(...) eu acabei de entrar na faculdade ai essa semana fui fazer uma revisão nos meu conhecimentos de matemática (...)
Para ajudar em sua revisão, eu recomendo que você assista as videoaulas do Nerckie no YouTube:
http://www.youtube.com/nerckie
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Fração] Ajuda em problema de fração.
por smlspirit » Sex Mai 18, 2012 01:17
- 3 Respostas
- 3816 Exibições
- Última mensagem por DanielFerreira

Dom Mai 20, 2012 17:06
Álgebra Elementar
-
- [Conjuntos] Confusão em teoria dos conjuntos numa questão.
 por Debora Bruna » Seg Jan 11, 2016 17:44
por Debora Bruna » Seg Jan 11, 2016 17:44
- 1 Respostas
- 8845 Exibições
- Última mensagem por DanielFerreira

Sáb Jan 23, 2016 16:44
Conjuntos
-
- [Conjuntos] Dúvida sobre conjuntos vazios
por ALPC » Qui Set 18, 2014 18:28
- 5 Respostas
- 6422 Exibições
- Última mensagem por adauto martins

Seg Set 22, 2014 15:44
Conjuntos
-
- [conjuntos]numeros racionais e conjuntos
por fenixxx » Ter Fev 28, 2012 21:35
- 3 Respostas
- 4732 Exibições
- Última mensagem por DanielFerreira

Sex Mar 02, 2012 00:04
Álgebra Elementar
-
- [Conjuntos] Problema de conjuntos com porcentagem
por Tibes » Qui Jan 31, 2013 14:29
- 1 Respostas
- 7963 Exibições
- Última mensagem por young_jedi

Sex Fev 01, 2013 12:39
Conjuntos
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


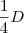 . Sobrou então
. Sobrou então 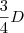 .
.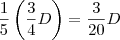 .
.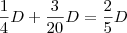 . Sobrou então
. Sobrou então 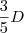 .
.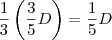 .
.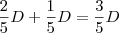 .
.