 por martinay » Sáb Out 29, 2011 02:52
por martinay » Sáb Out 29, 2011 02:52
Olá estou fazendo um exercício de área de superfície, segue abaixo o exemplo e onde parei.
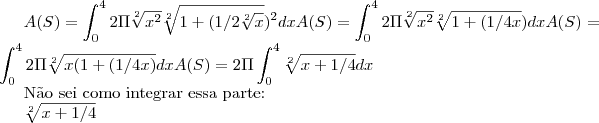
Se alguem puder me ajudar ficaria muito feliz... Obrigada
-
martinay
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Out 29, 2011 02:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: engenharia
- Andamento: cursando
 por LuizAquino » Sáb Out 29, 2011 10:01
por LuizAquino » Sáb Out 29, 2011 10:01
martinay escreveu:![A(S)=\int_{0}^{4}2\pi\sqrt[2]{x^2}\sqrt[2]{1+(1/2\sqrt[2]{x}})^2dx A(S)=\int_{0}^{4}2\pi\sqrt[2]{x^2}\sqrt[2]{1+(1/2\sqrt[2]{x}})^2dx](/latexrender/pictures/7e1ab03d8c09c539469094536d1b0394.png)
Se a função for
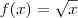
, então a integral correta seria:
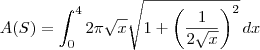
Note que você escreveu

ao invés de
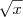
.
Além disso, você escreveu
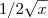
. Mas isso é o mesmo que
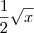
.
Por outro lado, se você escrever
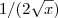
, então aí sim você tem algo equivalente a
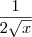
.
Note como usar os parênteses é importante.
martinay escreveu: ![A(S)=2\pi\int_{0}^{4}\sqrt[2]{x+1/4}dx A(S)=2\pi\int_{0}^{4}\sqrt[2]{x+1/4}dx](/latexrender/pictures/d64c5c94947236c5387fd045dbf291b8.png)
Não sei como integrar essa parte:
![\sqrt[2]{x+1/4} \sqrt[2]{x+1/4}](/latexrender/pictures/e74ad052e127f28e908a055da1ec0e34.png)
Basta fazer por substituição, escolhendo para isso
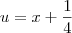
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Area de uma superficie de revolução
por miumatos » Seg Jun 18, 2012 01:34
- 1 Respostas
- 1993 Exibições
- Última mensagem por LuizAquino

Ter Jun 19, 2012 11:05
Cálculo: Limites, Derivadas e Integrais
-
- Area de Superfície de Revolução
por ariclenesmelo » Seg Out 22, 2012 22:00
- 3 Respostas
- 4684 Exibições
- Última mensagem por young_jedi

Ter Out 23, 2012 11:37
Cálculo: Limites, Derivadas e Integrais
-
- Superfície Esférica
por iarapassos » Ter Set 18, 2012 23:24
- 4 Respostas
- 4541 Exibições
- Última mensagem por young_jedi

Sex Set 21, 2012 18:17
Geometria Analítica
-
- Superfície Esférica
por iarapassos » Sex Set 21, 2012 17:24
- 1 Respostas
- 1547 Exibições
- Última mensagem por young_jedi

Sex Set 21, 2012 18:30
Geometria Analítica
-
- Integral de superfície
por AllanGeoffroy » Ter Fev 12, 2013 23:18
- 0 Respostas
- 911 Exibições
- Última mensagem por AllanGeoffroy

Ter Fev 12, 2013 23:18
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
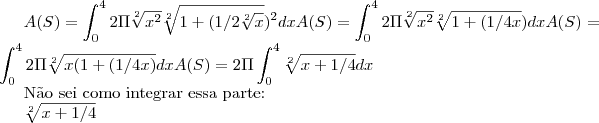

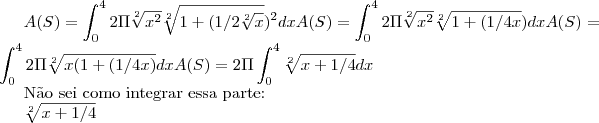

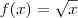 , então a integral correta seria:
, então a integral correta seria: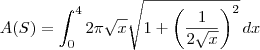
 ao invés de
ao invés de 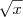 .
.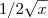 . Mas isso é o mesmo que
. Mas isso é o mesmo que 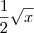 .
.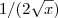 , então aí sim você tem algo equivalente a
, então aí sim você tem algo equivalente a 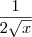 .
.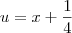 .
.
