elyjunior escreveu:(x? -2) ? 1 / 2x³ + 5x¹ =
(x? -2) ? (2x?³+ 5x?¹) =
O seu erro começou nesse passo.
Note que se a e b são não nulos, então tipicamente teremos
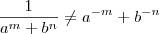
.
Por exemplo, note que:
(i)
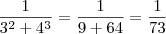
(ii)
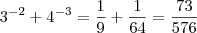
Comparando (i) e (ii), temos que
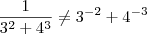
.
Para calcular esse limite, um procedimento correto é usar o que foi indicado por Renato_RJ.
ObservaçõesEm sua mensagem você escreveu:
elyjunior escreveu:lim x? - 2 / 2x³ + 5x =
x-> -?
Interpretando ao "pé da letra" isso é o mesmo que:
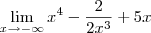
Entretanto, ao que parece você deseja na verdade o limite:
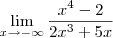
Nesse caso, você deveria ter escrito algo como:
lim (x? - 2) / (2x³ + 5x)
x-> -?
Note a importância de usar os parênteses (e os outros delimitadores) de forma adequada!
Aproveito ainda para indicar que você procure usar o LaTeX na escrita das notações matemáticas. Para saber mais a respeito disso, veja o tópico:
DICA: Escrevendo Fórmulas com LaTeX via BBCodeviewtopic.php?f=9&t=74Se precisar, use também o
Editor de Fórmulas disponível na criação de suas mensagens.
Por fim, eu gostaria de lhe dar uma dica.
Não direcione a sua mensagem para um usuário específico do fórum! Lembre-se que a ideia em um fórum é que todos podem ajudar!


 em evidência ?? Veja:
em evidência ?? Veja: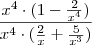
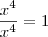 ) e o denominador a 0 pela esquerda, isto é, pelos números menores do que zero, logo o limite tenderá a
) e o denominador a 0 pela esquerda, isto é, pelos números menores do que zero, logo o limite tenderá a 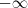 .
.
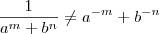 .
.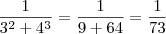
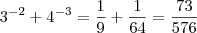
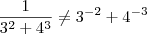 .
.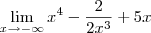
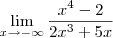

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.