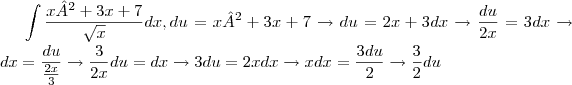
como terminar, se o u está correto ou não ?!
Primeira vez que posto, perdoem os erros.

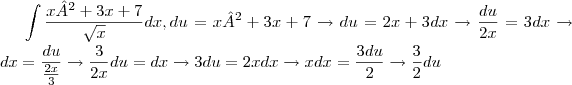

Klaubs escreveu:
como terminar, se o u está correto ou não ?!
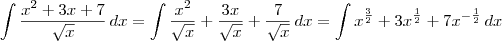
 .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes