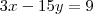
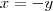
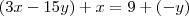

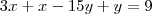
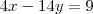
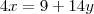
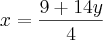
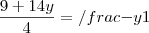
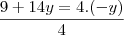
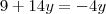
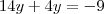

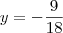
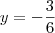
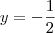
Fiz dessa forma, está certo o valor de
 ?
?
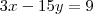
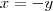
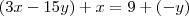

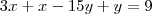
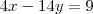
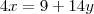
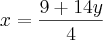
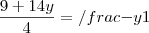
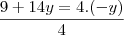
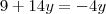
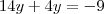

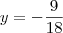


 ?
?
LuizCarlos escreveu:Estou tentando fazer esse exercício por meio do método da adição ! mas não estou conseguindo !
Essa é a forma correta do método de adição ?
Está certo o valor de?


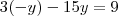
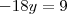
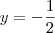
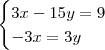

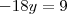


Caradoc escreveu:O resultado está certo, mas veja que você deu muita volta até chegar na resposta.
A estratégia no método da adição é tentar somar de modo que uma variável se cancele.
Do jeito que você fez, você apenas somou as duas equações e depois isolou uma das variáveis e substituiu na outra equação.
Se fosse para fazer por substituição, como você tem que x = -y então seria válido substituir o x multiplicando na primeira equação, por -y.
Assim:
Já para fazer o método da adição, você teria que multiplicar uma das equações (ou as duas) de modo conveniente para cancelar uma variável.
Por exemplo, poderiamos multiplicar a segunda equação por -3 e somar as equações:
O x cancelaria e ficaríamos com:
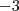 , ficando
, ficando 
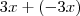 que no caso resultando Zero !
que no caso resultando Zero !
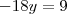
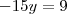
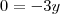



Caradoc escreveu:Para manter a igualdade, temos que somar em ambos os lados da equação a mesma quantia.
Eu somei o -3x do lado esquerdo da primeira equação e somei o 3y no lado direito da primeira equação.
Como na segunda equação -3x = 3y, o que eu fiz foi válido, pois apenas somei de cada lado da equação um mesmo valor, não alterando a igualdade.
A soma das equações seria assim:
Você pode pensar da mesma forma que faz uma soma com números, passe um risco em baixo das duas equações, coloque um sinal de igual alinhado e some tudo que está antes do igual nas 2 equações e todo que está depois.
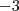
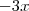
 da primeira equação
da primeira equação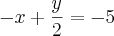
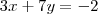

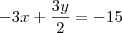
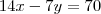

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)