 por AnaOliveira » Sáb Abr 30, 2011 16:54
por AnaOliveira » Sáb Abr 30, 2011 16:54
boa tarde... eu estou cm uma duvida numa funçao definida por ramos que é:
f(x,y) = x^3/(x^2 + y^2) se x > 0 e f(x,y) = x * ln(1+y^2) se x <= 0
Como verifico se a funçao é continua no ponto 0,0
pego no ramo d cima ou d baixo?
Na minha prespectiva deveria incluir o que tem o zero. Contudo estou co duvidas. Se me pudessem esclarecer.
-
AnaOliveira
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Abr 30, 2011 16:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistemas e Tecnologias da Informaçao
- Andamento: cursando
 por MarceloFantini » Sáb Abr 30, 2011 18:26
por MarceloFantini » Sáb Abr 30, 2011 18:26
Editado, explicado abaixo.
Editado pela última vez por
MarceloFantini em Sáb Abr 30, 2011 20:29, em um total de 1 vez.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Sáb Abr 30, 2011 18:55
por LuizAquino » Sáb Abr 30, 2011 18:55
Eu gostaria de recomendar que você assista ao vídeo:
04. Cálculo I - Limites e Continuidadehttp://www.youtube.com/watch?v=NOPEwktLxgwNesse vídeo há exercícios semelhantes a este, porém para funções de apenas uma variável.
Editado pela última vez por
LuizAquino em Dom Mai 01, 2011 12:35, em um total de 1 vez.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por AnaOliveira » Sáb Abr 30, 2011 20:26
por AnaOliveira » Sáb Abr 30, 2011 20:26
Agradeço a vossa ajuda!
Houve uma pessoa que entretanto me disse que para a resolução do problema teria de calcular o limite de x >0 e x < 0 e verificar se ambos sao iguais a zero.
Pelo que entendi tambem se pode resolver assim. Correcto?
Tinha a percepçao de que a continuidade em R era diferente de R2, por estarmos a trabalhar no plano e nao podermos seguir unicamente pela esquerda ou pela direita, devido a existirem varias formas de nos aproximarmos de 0.
Editado pela última vez por
AnaOliveira em Sáb Abr 30, 2011 20:33, em um total de 1 vez.
-
AnaOliveira
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Abr 30, 2011 16:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistemas e Tecnologias da Informaçao
- Andamento: cursando
 por LuizAquino » Sáb Abr 30, 2011 20:30
por LuizAquino » Sáb Abr 30, 2011 20:30
Houve uma pessoa que entretanto me disse que para a resolução do problema teria de calcular o limite de x >0 e x < 0 e verificar se ambos sao iguais a zero.
Pelo que entendi tambem se pode resolver assim. Correcto?
Tinha a percepçao de que a continuidade em R era diferente de R2, por estarmos a trabalhar no plano e nao podermos seguir unicamente pela esquerda ou pela direita, devido a existirem varias formas de nos aproximarmos de 0.
Deve-se analisar todos os caminhos como o colega Fantini disse abaixo.
Editado pela última vez por
LuizAquino em Dom Mai 01, 2011 12:38, em um total de 4 vezes.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por MarceloFantini » Sáb Abr 30, 2011 20:35
por MarceloFantini » Sáb Abr 30, 2011 20:35
Apaguei minha mensagem pois estava errado. Se não me engano, o limite não deve existir pois o limite do primeiro ramo não existe. Entretanto, isso é uma função de duas variáveis, então tecnicamente deveríamos mostrar por todos os caminhos?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Sáb Abr 30, 2011 20:37
por LuizAquino » Sáb Abr 30, 2011 20:37
MarceloFantini escreveu:Entretanto, isso é uma função de duas variáveis, então tecnicamente deveríamos mostrar por todos os caminhos?
Sim.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por AnaOliveira » Sáb Abr 30, 2011 20:41
por AnaOliveira » Sáb Abr 30, 2011 20:41
O primeiro limite existe! Eu provei pela definiçao que existe.! Sendo assim.. fiquei um pouco confusa. :S
-
AnaOliveira
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Abr 30, 2011 16:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistemas e Tecnologias da Informaçao
- Andamento: cursando
 por AnaOliveira » Sáb Abr 30, 2011 20:54
por AnaOliveira » Sáb Abr 30, 2011 20:54
Sim sim.. Contudo fiquei na duvida.. Sempre se resolve através da resolução dos dois limites correcto?
-
AnaOliveira
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Abr 30, 2011 16:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistemas e Tecnologias da Informaçao
- Andamento: cursando
 por MarceloFantini » Sáb Abr 30, 2011 21:11
por MarceloFantini » Sáb Abr 30, 2011 21:11
Sim, e os dois existem nesse caso. Como a função está definida em zero também e coincide com os limites, então ela é contínua no ponto.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por AnaOliveira » Sáb Abr 30, 2011 21:13
por AnaOliveira » Sáb Abr 30, 2011 21:13
Agradeço a ajuda!

-
AnaOliveira
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Abr 30, 2011 16:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistemas e Tecnologias da Informaçao
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função definida por ramos]Exercício
por fff » Qua Jan 22, 2014 10:51
- 0 Respostas
- 1729 Exibições
- Última mensagem por fff

Qua Jan 22, 2014 10:51
Funções
-
- [Derivada de função de duas variáveis] Dúvida numa passagem
por Fabio Wanderley » Sáb Dez 06, 2014 14:51
- 4 Respostas
- 3758 Exibições
- Última mensagem por adauto martins

Qua Dez 10, 2014 21:28
Cálculo: Limites, Derivadas e Integrais
-
- Função modulo por ramos
por joaofonseca » Seg Abr 30, 2012 17:13
- 1 Respostas
- 1541 Exibições
- Última mensagem por MarceloFantini

Sáb Mai 05, 2012 20:59
Funções
-
- [PA] Uma dúvida numa questão de PA
por rochadapesada » Qui Abr 04, 2013 22:08
- 3 Respostas
- 2639 Exibições
- Última mensagem por DanielFerreira

Dom Abr 07, 2013 20:28
Progressões
-
- Dúvida numa exercíco
por carlota_almada » Dom Dez 04, 2016 13:17
- 1 Respostas
- 2353 Exibições
- Última mensagem por Cleyson007

Seg Dez 05, 2016 20:35
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




















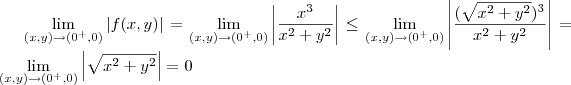
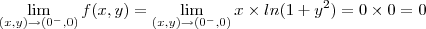
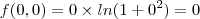


 .
.
 :
: