fbiochagas escreveu:Eu quero saber como é que se resultado do teste da idade bem como a metodologia para alcançar o resultado. Mande para o meu e-mail:
fbiochagas@yahoo.com.br
Olá
fbiochagas!
Espero ajudar.
Considerei uma "linha do tempo" para resolver este problema.
Veja esta representação:
x: "minha" idade atual
k: quantidade de anos decorridos entre o "passado" e o "presente";
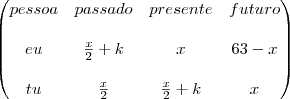
O fato é que o tempo decorrido para um é igual ao tempo decorrido para outro.
Sendo assim, podemos igualar estas diferenças de tempo.
Primeiramente, a diferença entre o "presente" e o "passado":
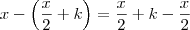
Daqui, obtemos que:

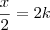
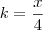
Agora, vamos utilizar este valor de
k encontrado (em relação a
x) e igualar a diferença entre o "futuro" e o "presente":
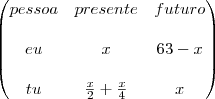
Temos que:
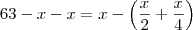
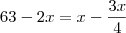
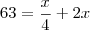
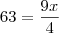


anos
("minha" idade atual)E para uma conferência, vejamos a "tua" idade:

anos ("tua" idade atual)
Mandei um link no seu e-mail, como pedido.
Abraço!




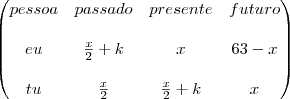
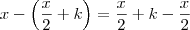

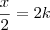
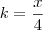
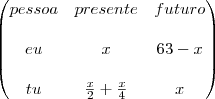
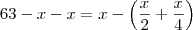
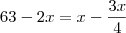
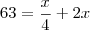
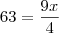

 anos ("minha" idade atual)
anos ("minha" idade atual) anos ("tua" idade atual)
anos ("tua" idade atual)
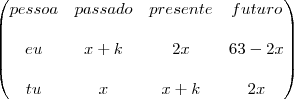

 ("minha" idade atual)
("minha" idade atual)

 .
.
 :
: