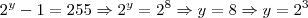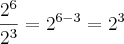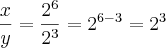por hian » Dom Nov 14, 2010 16:50
por hian » Dom Nov 14, 2010 16:50
(UF Santa Maria-RS) Se x = ((6@0))+((6@1))+..+((6@6)) e ((y@1))+((y@2))+..+((y@y))=225 então x/y vale:
a.5
b.6
c.8
d.7
e.9
esses @ é que eles tao em cima do outro por exemplo ((6@0)) = (6)
0
eu ja tentei de varias formas . o professor disse que a certa é a letra C e eu usei varias formulas como (n@k).(n-k/k+1)=(n@k+1)
t(k+1)=(n@k).x^n-k.y^k
e nao chego na alternativa me ajuda por favor T.T
-
hian
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Nov 14, 2010 15:46
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por VtinxD » Seg Nov 15, 2010 01:33
por VtinxD » Seg Nov 15, 2010 01:33
Pelo que me parece o enunciado esta errado , deveria ser 255 ao invés de 225.Porque:
*
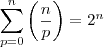
.Sendo então
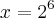
e
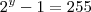
(perceba que esta faltando o

que vale sempre 1).Caso fosse 225 ,seria necessário a aplicação de logaritmo e o que provavelmente tornaria y um numero irracional ,que contraria a definição de numero binomial.
Caso esteja com o enunciado correto e ainda esteja com duvida vou postar o resto da minha resolução.
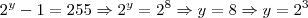
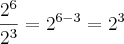
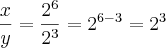
Espero ter ajudado.
*Não existe essa barra mas é o único jeito que sabei para escrever um binômio.
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
Voltar para Binômio de Newton
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão Complicada
por Kelvin Brayan » Dom Abr 24, 2011 11:01
- 2 Respostas
- 2892 Exibições
- Última mensagem por Kelvin Brayan

Dom Abr 24, 2011 15:01
Sistemas de Equações
-
- [questão complicada]
por JKS » Qui Jun 20, 2013 01:48
- 1 Respostas
- 2460 Exibições
- Última mensagem por adauto martins

Seg Jan 05, 2015 16:24
Números Complexos
-
- Questão complicada de volume.
por ravi » Qui Set 19, 2013 15:36
- 1 Respostas
- 1721 Exibições
- Última mensagem por young_jedi

Sex Set 20, 2013 21:39
Cálculo: Limites, Derivadas e Integrais
-
- Função implícita; Questão complicada!
por jemourafer » Qui Mai 17, 2012 18:30
- 4 Respostas
- 4250 Exibições
- Última mensagem por Fabio Wanderley

Sáb Mai 19, 2012 03:16
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] complicada
por fabriel » Sáb Nov 02, 2013 12:47
- 3 Respostas
- 2022 Exibições
- Última mensagem por e8group

Sáb Nov 02, 2013 19:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


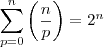 .Sendo então
.Sendo então 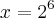 e
e 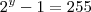 (perceba que esta faltando o
(perceba que esta faltando o  que vale sempre 1).Caso fosse 225 ,seria necessário a aplicação de logaritmo e o que provavelmente tornaria y um numero irracional ,que contraria a definição de numero binomial.
que vale sempre 1).Caso fosse 225 ,seria necessário a aplicação de logaritmo e o que provavelmente tornaria y um numero irracional ,que contraria a definição de numero binomial.