Desejamos encontrar as soluções naturais

para a equação
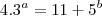
Ora,
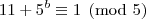
, para todo

. Logo
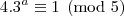
e como

é inversível a
 módulo cinco
módulo cinco, então devemos ter
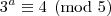
Analisando a
congruência módulo cinco para as potências de três, temos:
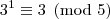
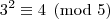
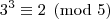
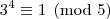
A partir daí as potências vão deixando os mesmos resíduos de modo a concluirmos que:
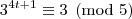
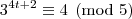
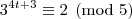
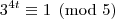
Assim, como
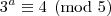
, então :
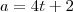
, com
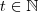
; que equivale a
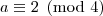
, isto é,

é par!
Analisemos a equação à luz
da congruência em módulo três: Para satisfazer a igualdade devemos ter
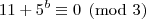
, isto é,
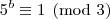
Analisando a
congruência módulo três para as potências de cinco, temos:
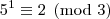
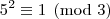
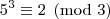
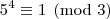
Analogamente, podemos concluir que :
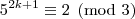
e
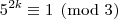
. Assim, como
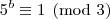
, então

, com
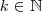
, isto é,

é par!
Como
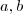
são ambos pares; sem perda de generalidade diremos que :
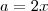
e

, com
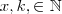
; então:
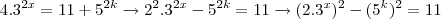
, isto é,
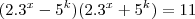
e como
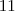
é primo, devemos ter:
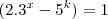
(i)
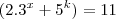
(ii)
já que o primeiro fator é sempre menor que o segundo fator e ambos são naturais devido as condições de contorno do problema.
Somando (i) e (ii) :
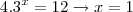
Subtraindo (i) de (ii):
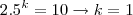
Assim só existe um único valor para

e um único valor para

que satisfazem, simultaneamente, a equação. Concluímos, portanto, que

é a única solução da equação.
Ps. Dava pra encurtar a resolução, mas como o Lorenzo pediu detalhes, achei melhor pormenorizar para ficar mais claro.


 para a equação
para a equação 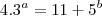
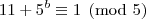 , para todo
, para todo  . Logo
. Logo 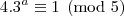 e como
e como  é inversível a
é inversível a 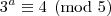
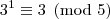
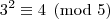
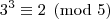
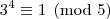
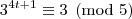
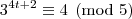
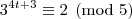
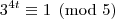
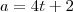 , com
, com 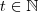 ; que equivale a
; que equivale a 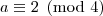 , isto é,
, isto é,  é par!
é par!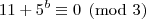 , isto é,
, isto é, 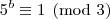
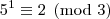
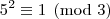
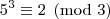
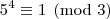
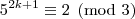 e
e 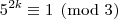 . Assim, como
. Assim, como  , com
, com 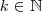 , isto é,
, isto é, 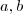 são ambos pares; sem perda de generalidade diremos que :
são ambos pares; sem perda de generalidade diremos que : 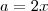 e
e 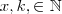 ; então:
; então: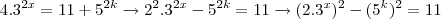 , isto é,
, isto é, 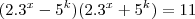 e como
e como 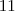 é primo, devemos ter:
é primo, devemos ter: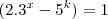 (i)
(i)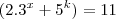 (ii)
(ii)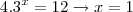
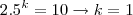
 é a única solução da equação.
é a única solução da equação.

 .
.



