raiz cubica (2x-1) - raiz cubica (x-1) = 1
(2x-1)^1/3 - (x-1)^1/3 = 1
oriunda de ex. de fisica
não consigo desenvolver, as respostas caso ajude são 1 e 2(14+3*raizquadrada 21)
muito obrigado a quem conseguir desenvolver



 )
)![\sqrt[3]{2x-1}-\sqrt[3]{x-1}=1 \sqrt[3]{2x-1}-\sqrt[3]{x-1}=1](/latexrender/pictures/9ad7addb1d67abd7eebc007168f886a1.png)
 então devemos ter que
então devemos ter que ![\sqrt[3]{2x-1}>\sqrt[3]{x-1} \sqrt[3]{2x-1}>\sqrt[3]{x-1}](/latexrender/pictures/7563c2e3b035c741a71ca9a5ed1d22cc.png) ou devemos ter que
ou devemos ter que ![\sqrt[3]{2x-1}<\sqrt[3]{x-1} \sqrt[3]{2x-1}<\sqrt[3]{x-1}](/latexrender/pictures/4e904686f58eddef150bf17774ff2a21.png) (pois podemos ter resultados negativos: raiz de índice ímpar). Para o 1º caso temos que
(pois podemos ter resultados negativos: raiz de índice ímpar). Para o 1º caso temos que 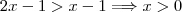 . Mas isso só ocorre se
. Mas isso só ocorre se 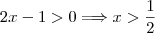 e
e 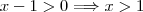 . Fazendo a intercessão (vamos interceder para que eu nunca mais cometa esse erro), digo interseção das inequações teremos que
. Fazendo a intercessão (vamos interceder para que eu nunca mais cometa esse erro), digo interseção das inequações teremos que  satisfaz o primeiro caso.
satisfaz o primeiro caso.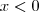 e
e 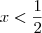 e
e 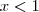 e a interseção dessas condições nos dá
e a interseção dessas condições nos dá 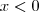 . Se
. Se  é solução dessa inequação então
é solução dessa inequação então ![k\in\mathbb R-[0,1] k\in\mathbb R-[0,1]](/latexrender/pictures/a8f99b6b60e719df037754349b99782c.png) . Logo a(s) solução(ões) dessa inequação não está entre zero e 1, inclusive.
. Logo a(s) solução(ões) dessa inequação não está entre zero e 1, inclusive.![\sqrt[3]{2x-1}-\sqrt[3]{x-1}=1 \sqrt[3]{2x-1}-\sqrt[3]{x-1}=1](/latexrender/pictures/9ad7addb1d67abd7eebc007168f886a1.png)
![(\sqrt[3]{2x-1}-\sqrt[3]{x-1})^3=1^3 (\sqrt[3]{2x-1}-\sqrt[3]{x-1})^3=1^3](/latexrender/pictures/f44f4bfa26fca549bd737632cc995370.png)
![(2x-1)-3\sqrt[3]{(2x-1)^2(x-1)}+3\sqrt[3]{(2x-1)(x-1)^2}-(x-1)=1 (2x-1)-3\sqrt[3]{(2x-1)^2(x-1)}+3\sqrt[3]{(2x-1)(x-1)^2}-(x-1)=1](/latexrender/pictures/c2b3ba752c2abb5e22f3b4b2d7cabdd5.png)
![2x-x-1+1-3\sqrt[3]{(2x-1)(x-1)}(\sqrt[3]{2x-1}-\sqrt[3]{x-1})=1 2x-x-1+1-3\sqrt[3]{(2x-1)(x-1)}(\sqrt[3]{2x-1}-\sqrt[3]{x-1})=1](/latexrender/pictures/1429091f075301a44f65f55b33e0ac94.png)
![x-1=3\sqrt[3]{(2x-1)(x-1)}(\sqrt[3]{2x-1}-\sqrt[3]{x-1}) x-1=3\sqrt[3]{(2x-1)(x-1)}(\sqrt[3]{2x-1}-\sqrt[3]{x-1})](/latexrender/pictures/bb901b1614c6cf6fbf57ef56679e53a4.png)
![\sqrt[3]{2x-1}-\sqrt[3]{x-1}=1 \sqrt[3]{2x-1}-\sqrt[3]{x-1}=1](/latexrender/pictures/9ad7addb1d67abd7eebc007168f886a1.png) . Então:
. Então:![x-1=3\sqrt[3]{(2x-1)(x-1)} x-1=3\sqrt[3]{(2x-1)(x-1)}](/latexrender/pictures/483636cd3a7b401ce34219c3f790ad70.png)
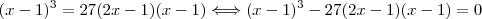
![(x-1)[(x-1)^2-27(2x-1)]\Longrightarrow x-1=0 \ $ou$ \ (x-1)^2-27(2x-1)=0 (x-1)[(x-1)^2-27(2x-1)]\Longrightarrow x-1=0 \ $ou$ \ (x-1)^2-27(2x-1)=0](/latexrender/pictures/48de1d3f57c3c7dfe7bb06fae3795481.png)
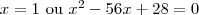

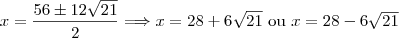
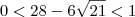 . Então esse resultado não convém, pois não obedece às condições do problema. Sendo assim, os valores de x que satisfazem essa equação são
. Então esse resultado não convém, pois não obedece às condições do problema. Sendo assim, os valores de x que satisfazem essa equação são 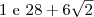 .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
